(I) Reflection about the line y = x (II) Transformation through a distance 2 unit along the positive direction of xaxis (III) Rotation through an angle π/4 about the origin in the a counter clockwise direction Then, the final position of the point is given by the coordinatesProgram to illustrate the implementation of 3D Rotation Transformation along xaxis 4 Reflection along with the line In this kind of Reflection, the value of X is equal to the value of Y We can represent the Reflection along yaxis by following equation Y=X, then the points are (Y, X) Y= – X, then the points are ( – Y, – X) We can also represent Reflection in the form of matrix – Homogeneous Coordinate

Reflection Mathbitsnotebook A1 Ccss Math
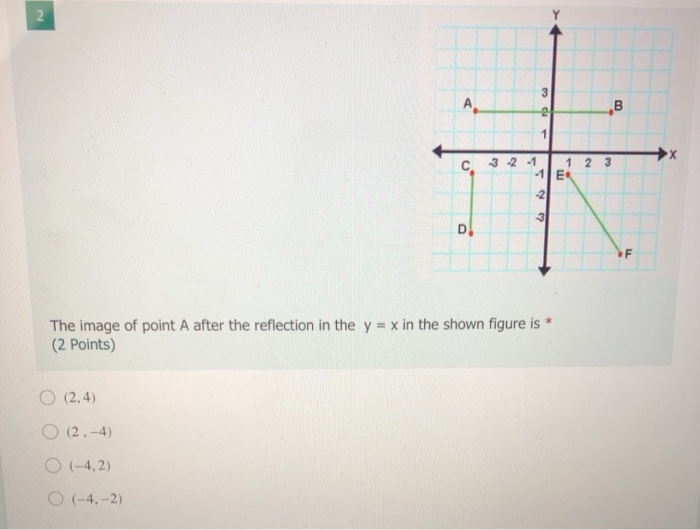
Reflection along the line y=x
Reflection along the line y=x-Reflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinates Question The equation of a circle with centre (0,5) and radius of length 2 units The circle is reflected along the line y=x I already found the equation of the circle which is x 2 (y5) 2 = 2 2 and the radius of the reflection circle which will be 2 But, I don't really know how to find the coordinates for the reflection circle




Reflection Over The Line Y X Math Showme
Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxis The last step is the rotation of y=x back to its original position that is counterclockwiseExpress reflection in the line y=x as the composition of a rotation followed by reflection in the line y=x ( done by matrices ) Question Express reflection in the line y=x as the composition of a rotation followed by reflection in the line y=x ( done by matrices )Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange
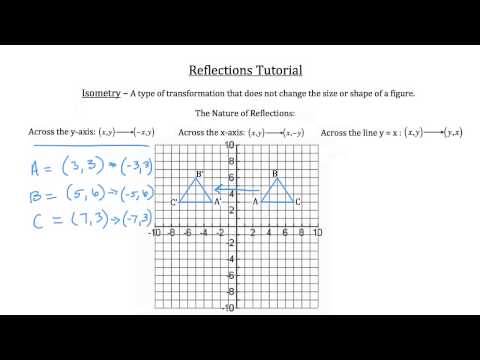
$\begingroup$ Reflecting a function along the line y = x is the same as computing the inverse of the function So use a method for computing the inverse of a function to find the reflection about the line y = x $\endgroup$ –Reflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A ( Since, we know that the conjugate of a point is the reflection of the point about XAxis In order to be able to use this fact, we will first perform translation (making A as the origin in the new system) and then rotating the coordinate axes in such a way that the line becomes the XAxis in the new coordinate system
Reflection of a Point In these printable worksheets for grade 6 and grade 7 reflect the given point and graph the image across the axes and across x=a, y=b, where a and b are parameters Choose the Correct Reflection This practice set tasks 6th grade and 7th grade students to identify the reflection of the given point from the given optionsApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine theReflection Symmetry Transformations Rotation Translation Geometry Index



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com




Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
Answer (1 of 4) Reflections in the coordinate plane When you reflect a point across the xaxis, the xcoordinate remains the same, but the ycoordinate is transformed into its opposite (its sign is changed) If you forget the rules for reflections when graphing, simply fold your paper along tAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxisIf (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed;




Graph The Image Of Jkl After A Reflection Over The Line Y X Brainly Com




Reflection Over A Line Expii
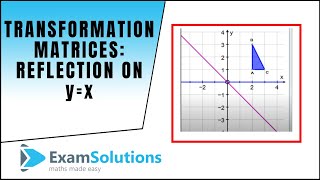
Graphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the xaxis or the yaxisWhen we multiply the parent function latexf\left(x\right)={b}^{x}/latex by –1, we get a reflection about the xaxisWhen we multiply the input by –1, we get a reflection about the yaxisFor example, if we begin by graphing the parentThis video explains what the transformation matrix is to reflect in the line y=x This video explains what the transformation matrix is to reflect in the line y=x Show by using matrix method that a reflection about the line #y=x# followed by rotation about origin through 90° ve is equivalent to reflection about yaxis?




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q
A ray of light along x 3 y = 3 gets reflected upon reaching xaxis, the equation of the reflected ray is View solution Plot D ( − 2 , − 5 ) on the graph and its reflection yaxisReflections and Rotations Summary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line ySee the answer Show transcribed image text Expert Answer 100% (2 ratings)



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line
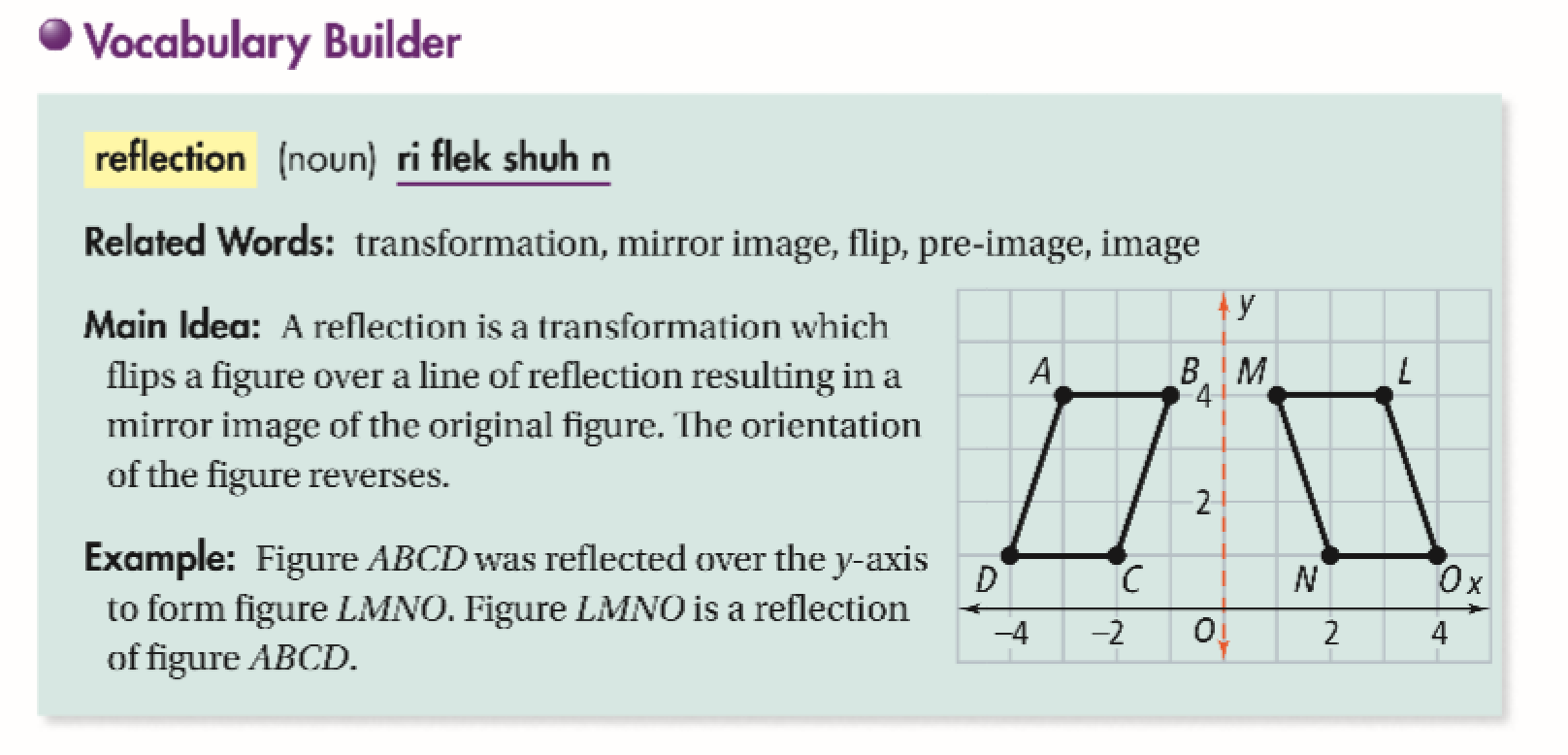
Reflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflectionDetermining reflections (advanced) CCSSMath HSGCOA5 Transcript Sal is given two line segments on the coordinate plane, and determines the reflection that maps one of them into the other Google Classroom Facebook TwitterReflection A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrix



Math Alive Geometry 1



Solved 1 After The Reflection Over The Line Y X The Image Chegg Com
Answer (1 of 4) You really need to draw this out to get a real feel for the answer and what is happening Think of y=2 as a horizontal mirror line Cutting through the yaxis at 2 The point (3,1) will reflect from below the xaxis over the mirror line and end up, above it, keeping the xcoor The point (4, 1) undergoes the following two successive transformations (i) Reflection about the line y = x (ii)Translation through a distance 2 units along the positive xaxis Then the final coordinates of the point areThe resulting orientation of the two figures are opposite



What Is The Reflection Image Of 5 3 In The Line Y X Socratic




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
Program of reflection in y Axis;Line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line is indeed negativeAnd so we want thes two angles to be the same, so they'll be high fourths or 45 degrees And if we kept drawing that blue line down, for instance, then that would end up having an equation Why is equal to Positive X and then minus one would be the Y intercept there So this would be the equation of the line that would reflect off of the X axis




Reflection Over Y X Math Geometry Showme




Reflections Across Y X Geogebra
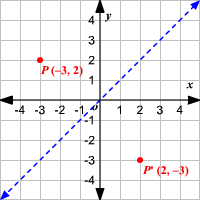
A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you wantGeometry 1 Answer Ultrilliam See below Explanation Reflection about the line #y = x# The effect of this reflection is to switch the x and y values of the reflected pointQuestion Prove That The Reflection Along The Line Y = X Is Equivalent To Reflection Along The Xaxis Followed By Counter Clockwise Rotation By 90 Degree This problem has been solved!




Which Graph Shows A Reflection Across The Line Y X Brainly Com



Reflecting Points Video Reflections Khan Academy
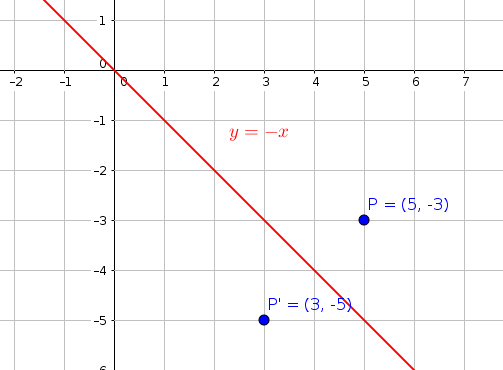
The linear transformation rule (p, s) → (r, s) for reflecting a figure over the oblique line y = mx b where r and s are functions of p, q, b, and θ = Tan 1 (m) is shown below Finding the linear transformation rule given the equation of the line of reflection equation y = mx b involves using a calculator to find angle θ = Tan 1 (mUse the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the form y = m x b y = m x b m = − 1 m = 1 b = 0 b = 0A line drawn from (1,1) perpendicular to the given line yx = 0 is y = xThe two lines intersect at (0,0)So, perpendicular distance of (1,1) from (0,0) is 11 = 2 We thus need the point on the line y = x, at a distance of 2 as a reflection of (1,1)Let the point be (a,a)a2 a2 = 2 ⇒ a2 = 1a = ±1Thus, reflection of the point (1,1) along the
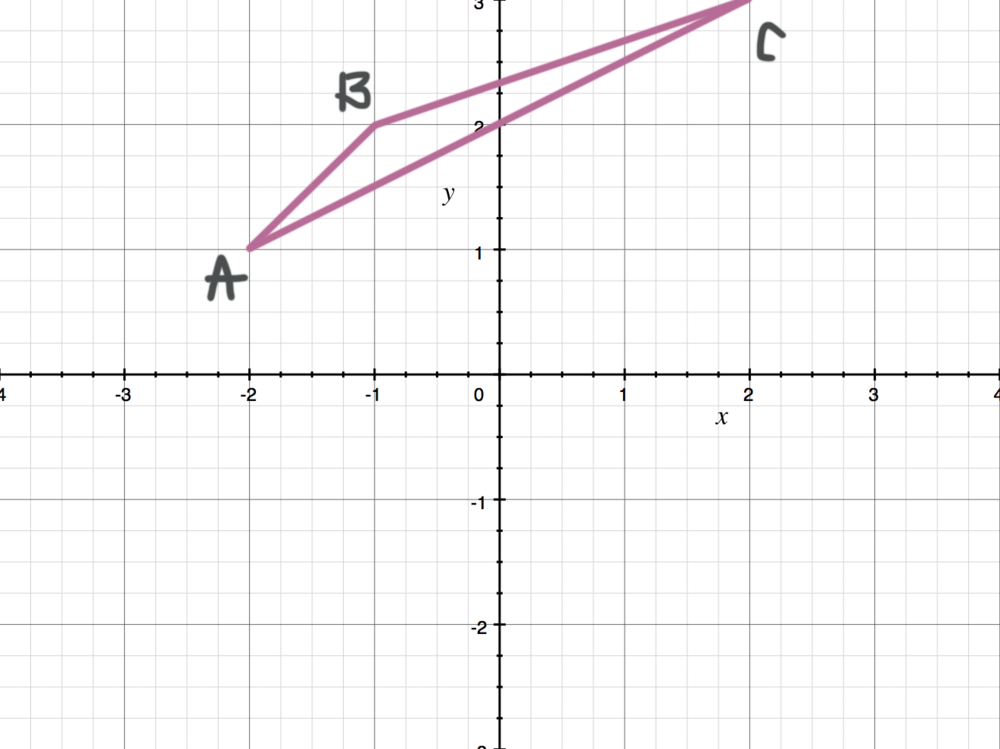



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



What Is The Reflection Of The Point 3 1 In The Line Y 2 Quora
3 people liked this ShowMe Flag ShowMe Viewed after searching for reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMe Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size 🔴 Answer 2 🔴 on a question Identify the reflection rule in the given figure A Reflection along the line y = –1 B Reflection along xaxis C Reflection along y = 1 D Reflection along yaxis the answers to answerhelpercom




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Reflection Rules How To W 25 Step By Step Examples
Reflect the figure across the line y = x the line y = x Show the mapping of ordered pairs by listing the preimage and image points 5 Draw and name the line of reflection 6 Draw and name the line of reflection for the figures for the figures Title Reflections Worksheet Author MISD Created Date PMThis is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableProgram to illustrate the implementation of Reflection Transformation about the line y=x and y=x;
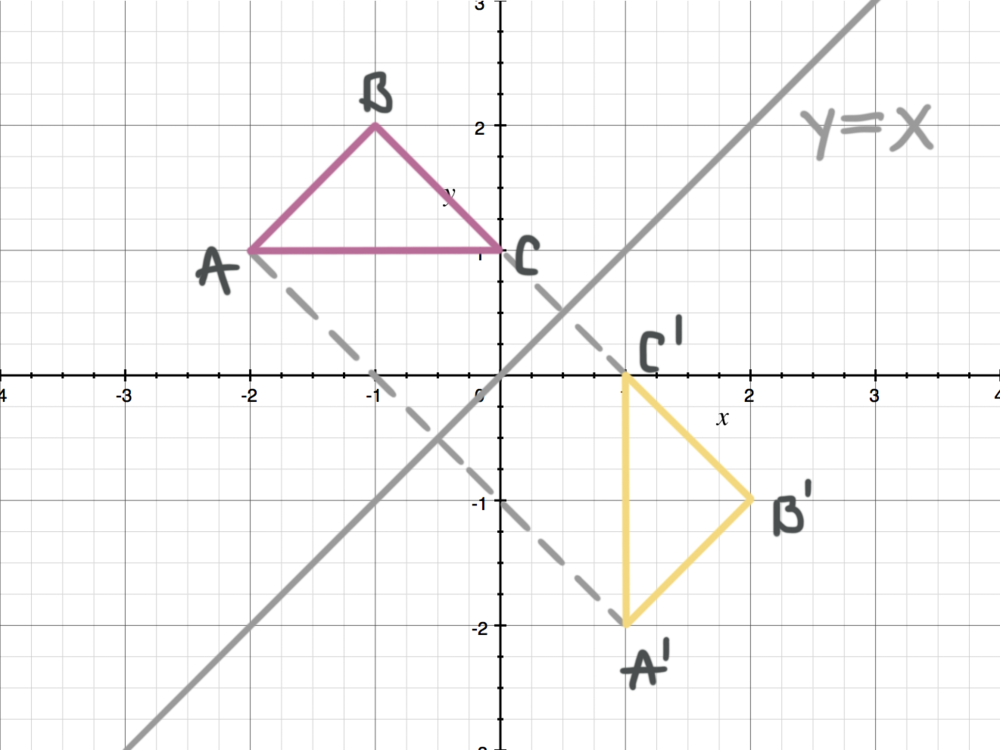



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Lesson On Line Of Reflection Y X
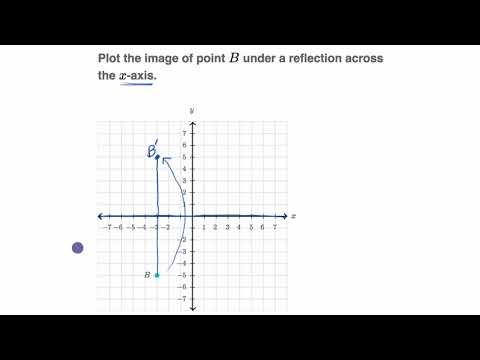
So this problem has to do with Slope and remember to get the slope of a line You take the difference in the UAE values over the difference in the X values so we can get the slope between the point with coordinates to three on the point with coordinates 00 three minus zero is the difference in why to For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflectionLearn about reflection in mathematics every point is the same distance from a central line Show Ads When the mirror line is the yaxis we change each (x,y) just fold the sheet of paper along the mirror line and then hold it up to the light !




Reflections Through The Axes And The Lines Y X And Y X Geogebra



1
The most common reflections are reflections in the xaxis (y = 0), the yaxis (x = 0), the line x = c, the line y = c, the line y = x and the line y = −x A Reflection in the XAxis The shape below has been reflected in the xaxis Each point on the image is the same perpendicular distance from the line of reflection as the object Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a Solution This video demonstrates how to reflect a figure over the line y=x It shows two methods of reflecting over y=x The video shows how to count towards the y=x




Reflections Ck 12 Foundation




Reflection Rules How To W 25 Step By Step Examples
Here we have a sketch of the figure and were asked to find the value of X If why is 42?The reflection of the point (x, y) across the line y = – x is (y, x) Reflection in a Point A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figure For every point in the figure, another point is found directly opposite to it on the other side Under the pointProgram to illustrate the implementation of Reflection Transformation about xaxix, yaxis and wrt origin;




Reflection Mathbitsnotebook A1 Ccss Math
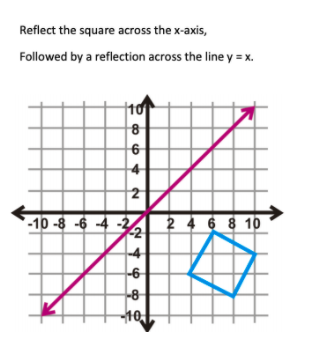



Solved Reflect The Square Across The X Axis Followed By A Chegg Com




Reflections Ck 12 Foundation
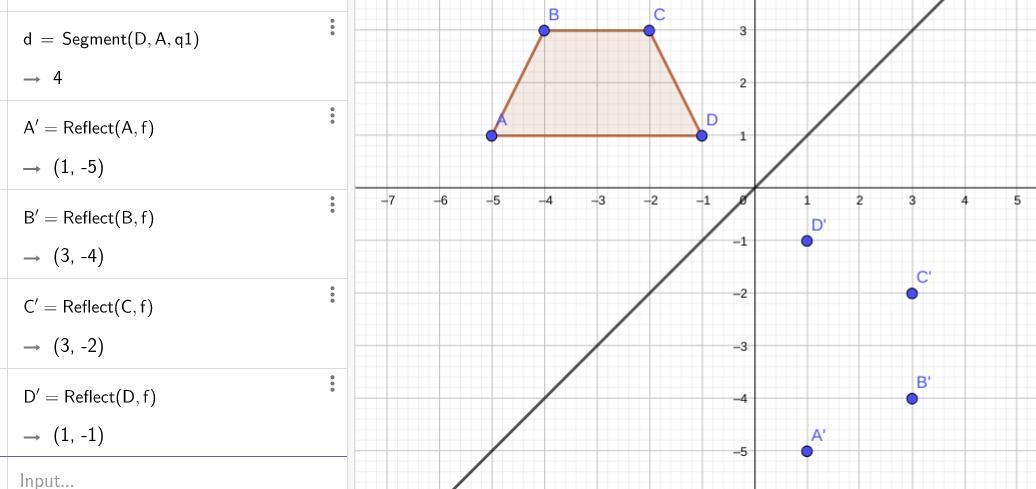



Trapezoid Abcd Is Reflected Over The Line Y X What Rule Shows The Input And Output Of The Reflection And What Is The New Coo



Reflection Of A Point In A Line Msrblog




Reflection Mathbitsnotebook A1 Ccss Math



Solution Describe The Relationship Between The Graph Of Y 2x 1 And It 39 S Reflection Across The Line Y X
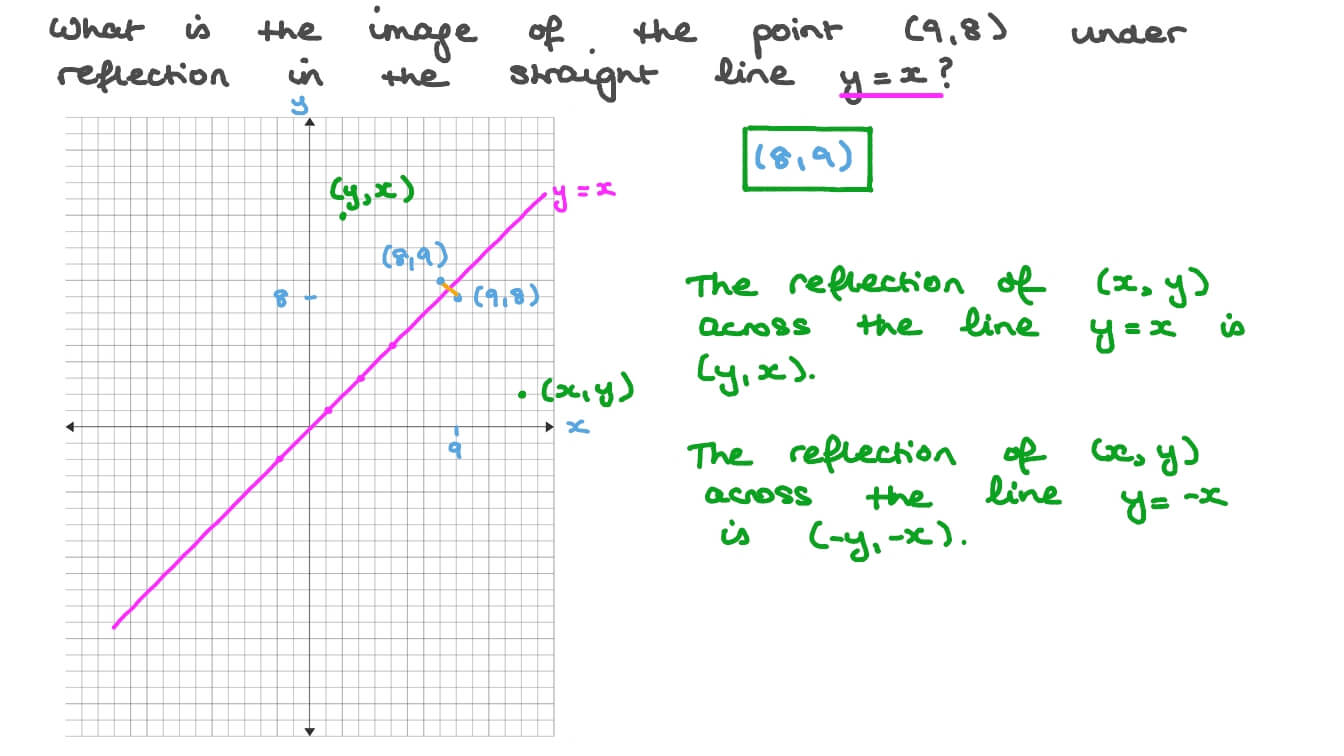



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflection Mathbitsnotebook A1 Ccss Math




Reflection Transformation Matrix




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Common Reflections Key Stage 3




Transformations Of Graphs



Illustrative Mathematics
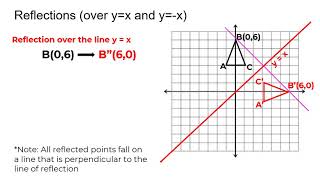



Reflection Over The Y X Line Youtube



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora
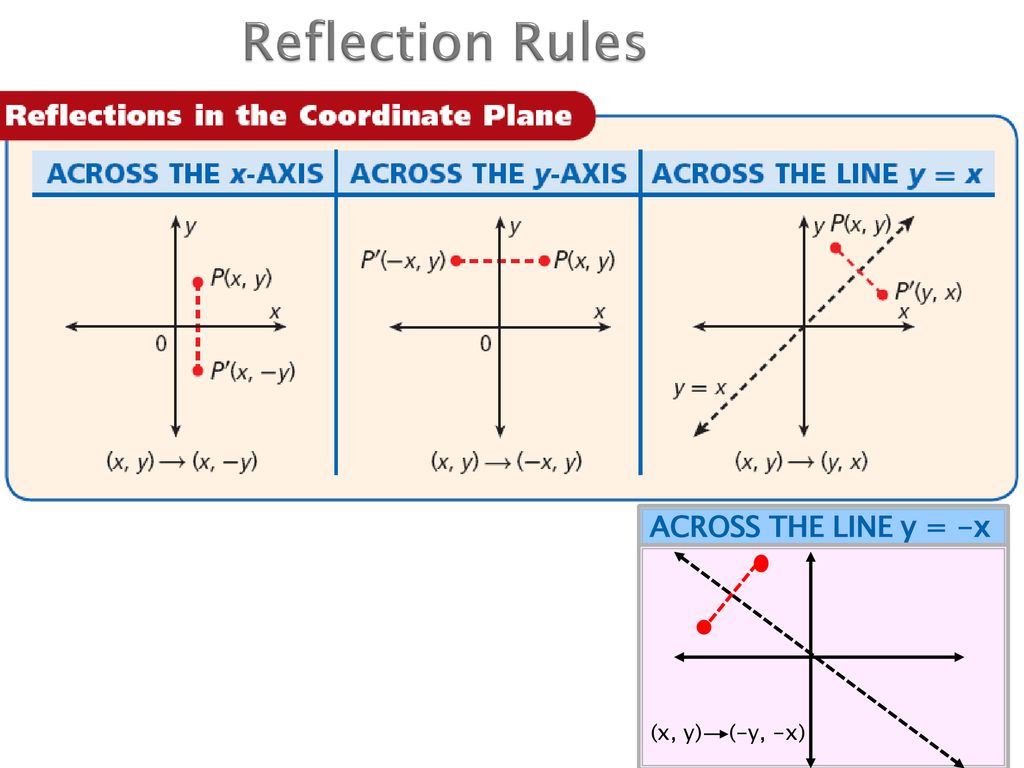



Pearson Unit 2 Topic 8 Transformational Geometry 8 2 Reflections Pearson Texas Geometry C 16 Holt Geometry Texas C Ppt Download




Reflection In The Line Y X Transformation Matrix Youtube




Reflection Over The Line Y X Math Showme



Translation Math



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Rules For Reflections Read Geometry Ck 12 Foundation




Reflection Over The Line Y X Youtube




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



What Does It Mean To Reflect Over The Y X Line Quora




Reflection Over The Y X Line Youtube
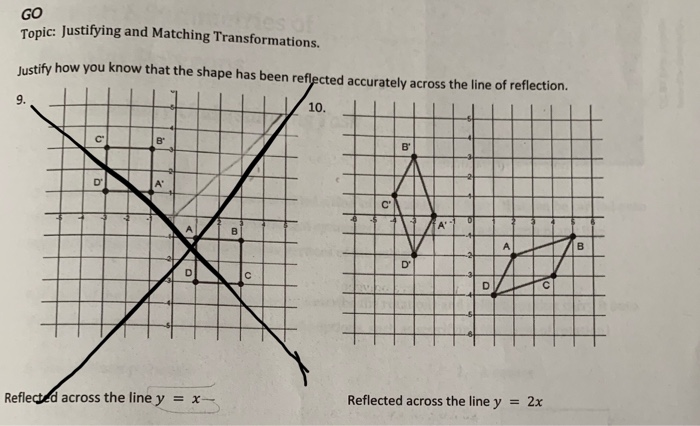



Solved Go Topic Justifying And Matching Transformations Chegg Com




How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium



View Question Reflection Across The Line Y X



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs



Reflections




Geometry Reflection Across Y X Youtube




Reflection Over The Line Y X Geogebra




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



Reflections Reflection In The Line Y X Revisely




Learn About Reflection Over The Line Y X Caddell Prep Online
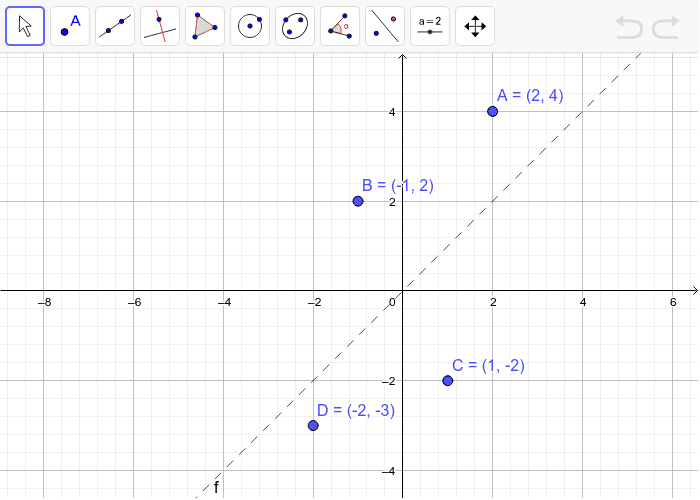



Reflecting In The Line Y X 2 Geogebra
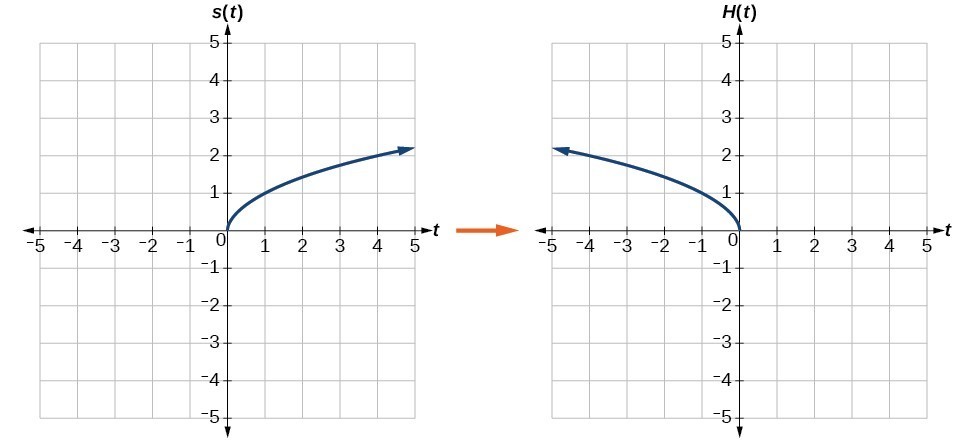



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
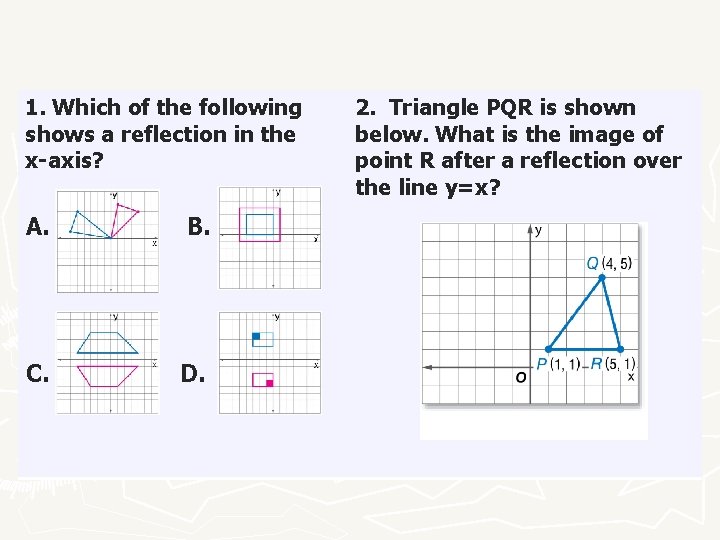



Warmup Reflect Triangle Abc Across The Line Y



Coordinate Plane




Reflection Transformation Matrix
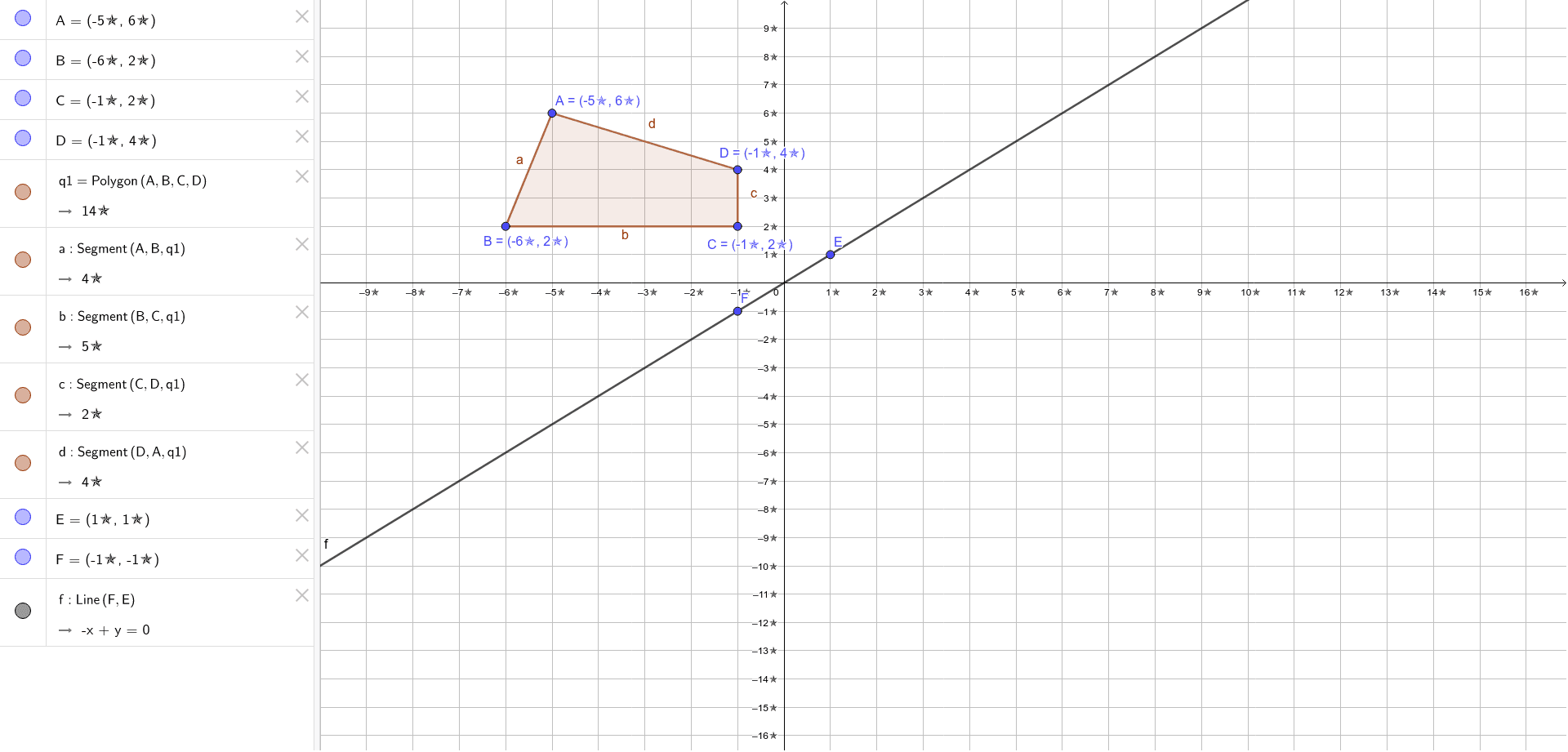



Reflection Across The Line Y X Geogebra




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3
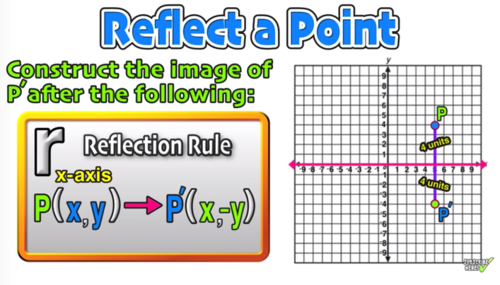



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Mathbitsnotebook A1 Ccss Math



Math Alive Geometry 1
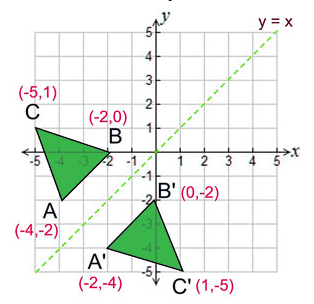



Reflection Definition Reflection In The Coordinate Plane
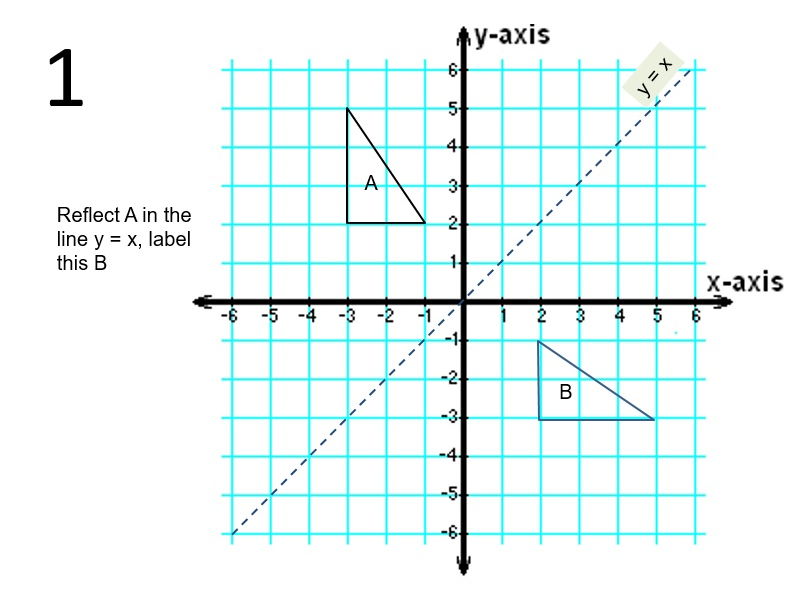



Diagonal Reflections In The Line Y X Teaching Resources
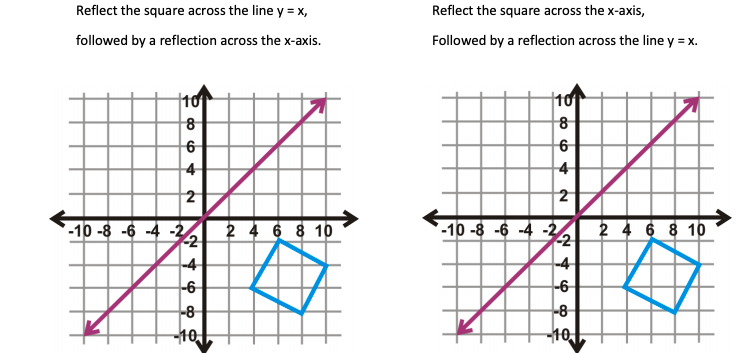



Solved Reflect The Square Across The Line Y X Followed By Chegg Com
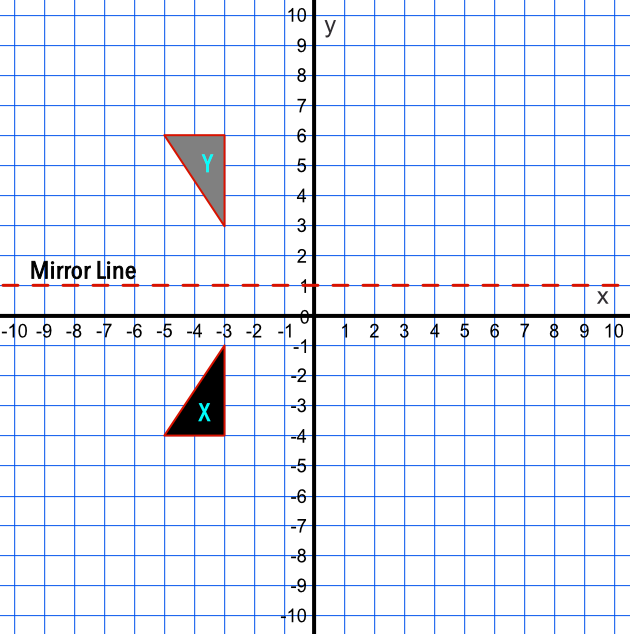



Reflection




Transformation Reflection Over The Line Y X Youtube




Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com



1




Reflecting Shapes Video Reflections Khan Academy




Picture Of Reflection Across Y Axis Reflection Math Math Reflection
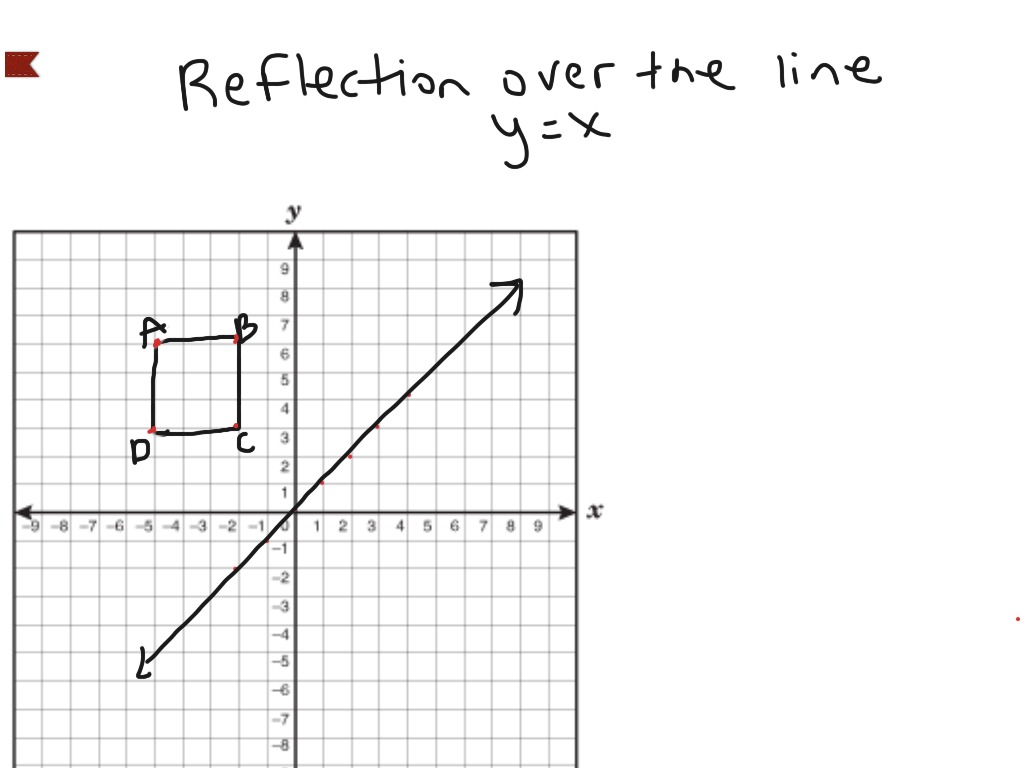



Reflection Over The Line Y X Math Showme




Reflection Over Y 2 With Rule Educreations



What Is The Image Of 2 5 Reflected Across X 2 Socratic




Reflection Mathbitsnotebook A1 Ccss Math




D Reflection Across Y X Brainly Com




Transformations Boundless Algebra
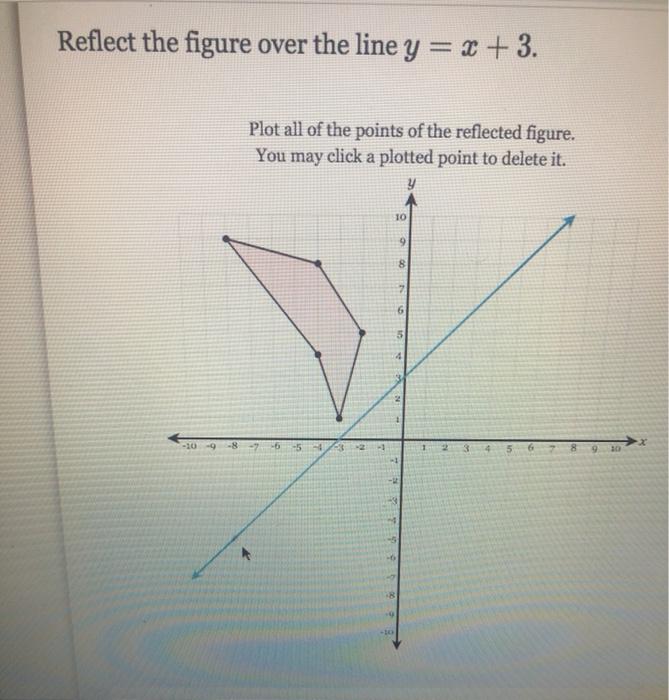



Solved Reflect The Figure Over The Line Y X 3 Plot All Chegg Com




Reflection Transformation Matrix




How To Find A Reflection Image




Write The Coordinates Of The Vertices After A Reflection Over The Line Y 3 Brainly Com



Ixl Reflections




Reflections Geometry Abroad




Reflection




Reflection In The Line Y X Geogebra




Rules For Reflections Ck 12 Foundation



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero




How To Find A Reflection Image



Solution What Is The Image Of A 3 1 After A Reflection First Across The Line Y 3 And Then Across The Line X 1
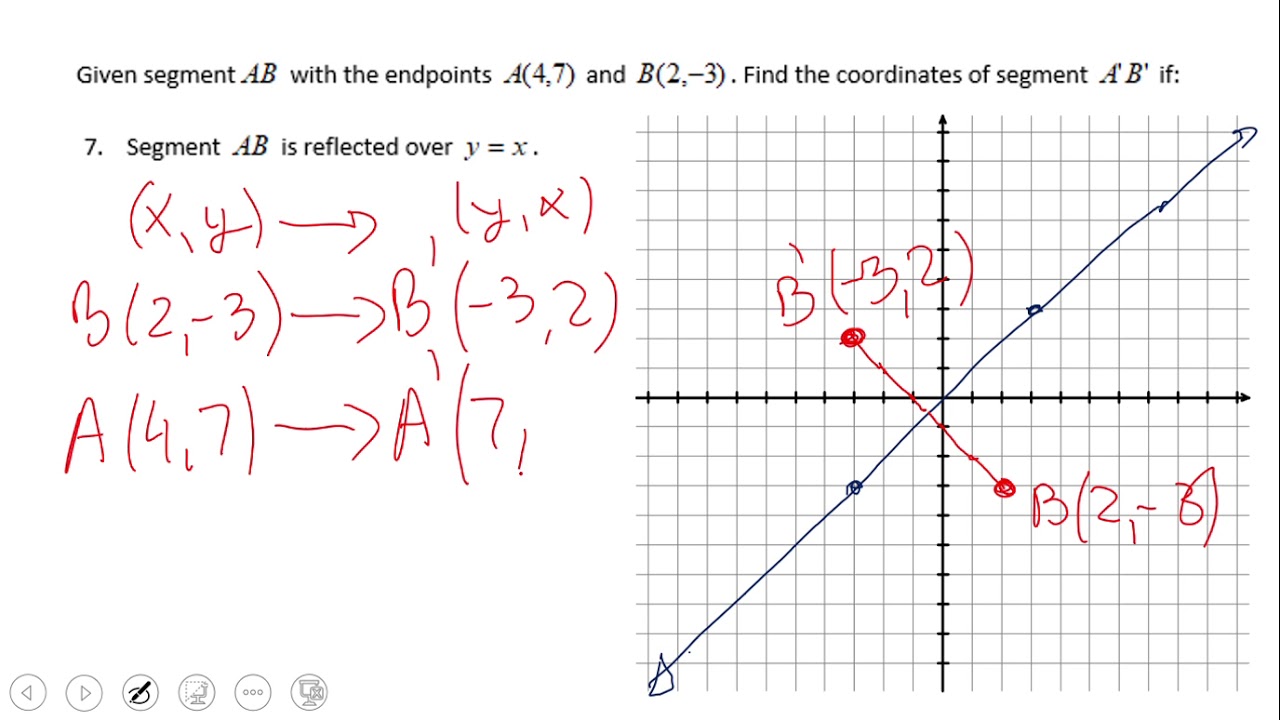



Reflection Over Y X And Y X Youtube




What Is A Line Of Reflection Virtual Nerd




Geometry Transformations


