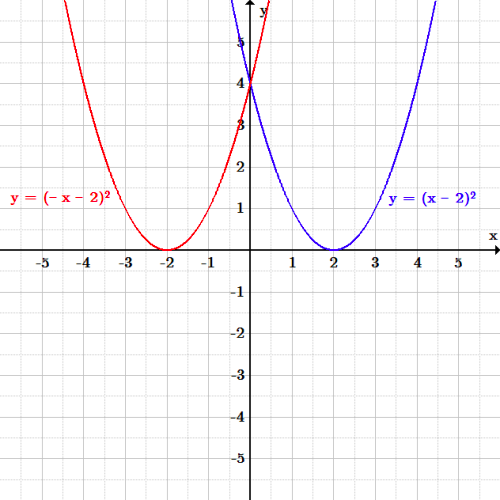
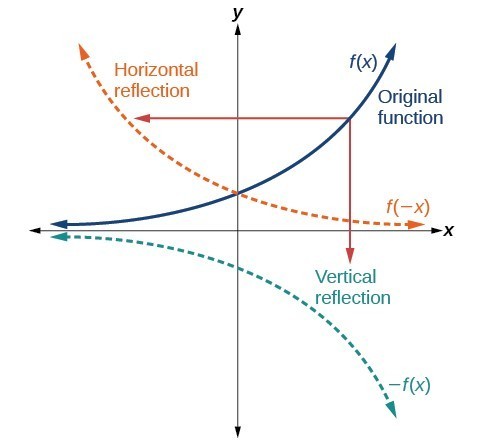
Reflecting Over the xaxis Another effect of " a " is to reflect the graph across the x axis When the parent function f (x) = x2 has an a value that is less than 0, the graph reflects across the x axis before it is transformed The graph below represents the function f (x) = x2 In function notation, this reflection is represented by aReflection across the yaxis y = f (− x) y = f(x) y = f (− x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaAnother effect of "a" is to reflect the graph across the xaxisWhen the parent function f(x) = x 2 has an avalue that is less than 0, the graph reflects across the xaxis before it is transformedThe graph below represents the function f(x) = x 2 In function notation, this reflection is represented by a negative outside the function f(x)If the negative is inside the function notation
Graphs Of Exponential Functions
Reflection over x axis vs y axis equation
Reflection over x axis vs y axis equation-To reflect a shape over an axis, you can either match the distance of a point to the axis on the other side of using the reflection notation To match the distance, you can count the number of units to the axis and plot a point on the corresponding point over the axis You can also negate the value depending on the line of reflection where the xvalue is negated if the reflection is overSummary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)




Reflection
The graph of \ (h (x) = \dfrac {1} {2}\abs {x}\) is a vertical compression of the basic graph \ (y = \abs {x}\) by a factor of \ (2\text {,}\) combined with a reflection about the \ (x\)axis You may find it helpful to graph the function in two steps, as shown in Figure263 Figure 263Example 3 Triangle PQR has the vertices P(2, 5), Q(6, 2) and R(2, 2) Find the vertices of triangle P'Q'R' after a reflection across the xaxis Then graph the triangle and its image Solution Step 1 Apply the rule to find the vertices of the imageSuch equations will depend upon which line is used as the line of reflection By far the easiest lines to use for this purpose are the xaxis, the yaxis, the line x = y, and the line x = y Figures 4 and 5 show two such reflections In Figure 4 the line of reflection is the yaxis As the figure shows, the ycoordinates stay the same, but the
Reflection across the xaxis y = − f (x) y = f(x) y = − f (x) The concept behind the reflections about the xaxis is basically the same as the reflections about the yaxis The only difference is that, rather than the yaxis, the points are reflected from above theAnother transformation that can be applied to a function is a reflection over the latexx/latex– or latexy/latexaxis A vertical reflection reflects a graph vertically across the latexx/latexaxis, while a horizontal reflection reflects a graph horizontally across the latexy/latexaxis The reflections are shown in Figure 9Reflecting functions examples CCSSMath HSFBF Transcript We can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems
A reflection can be done through yaxis by folding or flipping an object over the y axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directionsApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflectionXaxis y= log (x) reflection across the The function has also been vertically compressed by a factor of ⅓, shifted 6 units down and reflected across the xaxis Write the new equation of the logarithmic function according to the transformations




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Over The X And Y Axis The Complete Guide Mashup Math
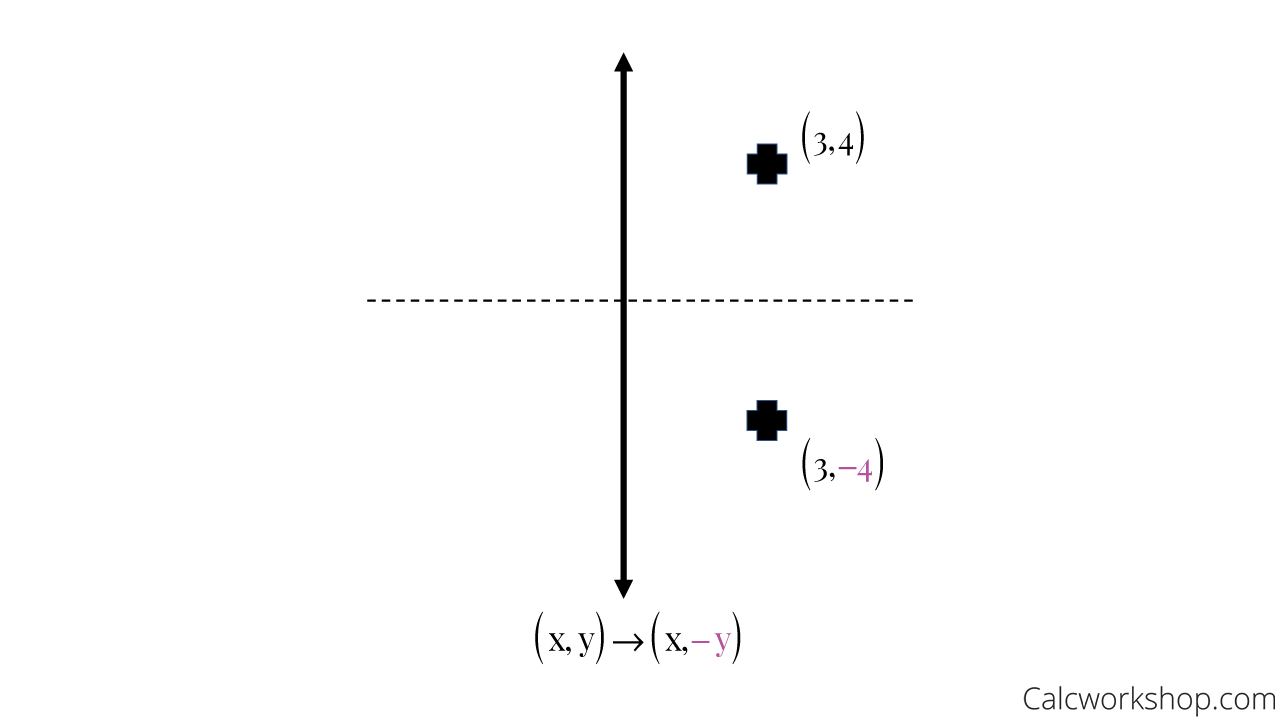
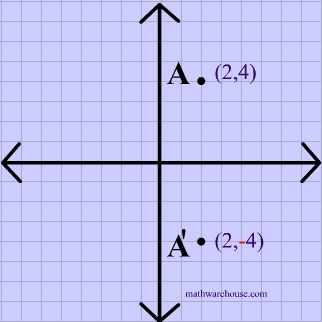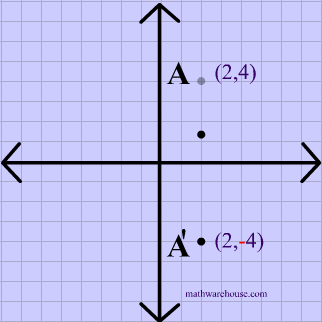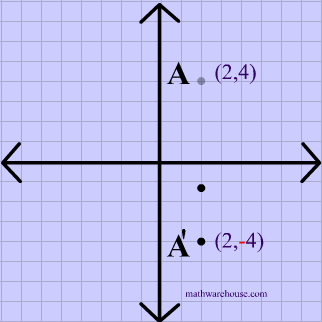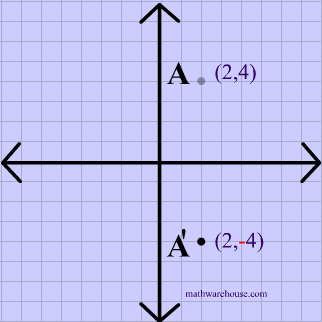
The rule for a reflection over the x axis is ( x , y ) → ( x , − y ) Reflection in the y axis A reflection of a point over the y axis is shown The rule for a reflection over the y axis is ( x , y ) → ( − x , y ) Reflection in the line y = x A reflection of a point over the line y = x is shownTherefore, the reflection of the point (x, y) across Xaxis is (x, y) Reflection over Yaxis When a point is reflected across the Yaxis, the Ycoordinates remain the same But the Xcoordinates is transformed into its opposite signs Therefore, the reflection of the point (x, y) across Yaxis is (x, y) Reflection over Y = XReflection over yaxis T(x, y) = (x, y) Reflection over line y = x T(x, y) = (y, x) Rotations Turning Around a Circle A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotation You can rotate your object at any degree measure, but 90° and 180° are two of the most common



Transformations Boundless Algebra



Transformations Boundless Algebra
Answer choices y=0 xaxisStep 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 3 The formula for this is {eq}(x,y) \rightarrow (x,y) {/eq} To reflect an equation over the yaxis, simply multiply the input variable by 1 {eq}y=f(x) \rightarrow y=f(x) {/eq}



Assignment 11



Reflection Rules How To W 25 Step By Step Examples
Question 9 SURVEY 60 seconds Q What is the equation of the line of reflection that reflects shape A onto shape C?Identifying Symmetry in Equations Graphs of Equations on a coordinate plane can have symmetry with respect to the XAxis, YAxis, and/or the Origin Some equations have no symmetry, and some equations have multiple types of symmetry Each type of symmetry can be determined individually using either graphical or algebraic test methodsFrom this expression it is clear that the all the values of y coordinate axis are changed by their negative values and the values of x coordinate axis are unchanged Therefore, the final result will show a flip over along the x axis If there is a point (x, y) on a plane, then its vertical reflection can be denoted by the point (x, y)



Reflect Function About Y Axis F X Expii
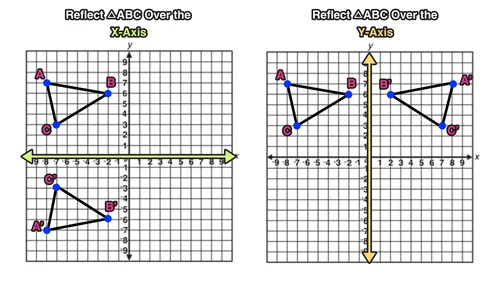



Reflection Over The X And Y Axis The Complete Guide Mashup Math
To reflect the absolute value function over the xaxis, we simply put a negative sign before the symbol (in this case the absolute value bars) Our new equation would be y = Ix3I Check the graphs in your calculator, they should look like a mirror image of each other, reflected over the xaxis Now try reflecting reciprocal y = 1/x 4 What is the equation of the function f(x) = 3x 6 reflected across the yaxis?The shapes are the same The graph of is a reflection over the xaxis of the graph of Fold the graph of over the xaxis so that it would be superimposed on the graph of Every point on the graph of would be shifted up or down twice it's distance from the xaxis For example, the point (a, 8) is located 8 units up from the xaxis
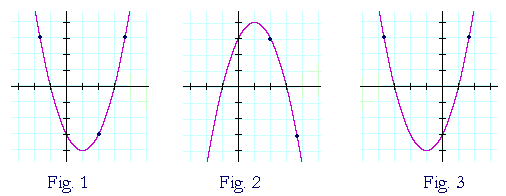



Reflections Of A Graph Topics In Precalculus



2
When reflecting over the xaxis, the function f(x) becomes f(x) For instance, y = 3x^2 would become y = (3x^2) On the other hand, when we reflect the function f(x) over the yaxis it becomes fOn this lesson, you will learn how to perform reflections over the xaxis and reflections over the yaxis (also known as across the xaxis and across the yaStart studying Reflecting points over the x and y axes Learn vocabulary, terms, and more with flashcards, games, and other study tools Search Browse Create Log in Sign up Log in Sign up Reflecting points over the x and y axes STUDY Reflect (3,4) over the y axis (2,6) Reflect (2,6) over the x axis



1
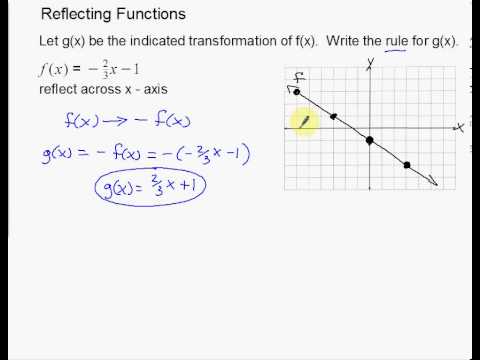



Linear Reflections Across X And Y Axis Example Youtube
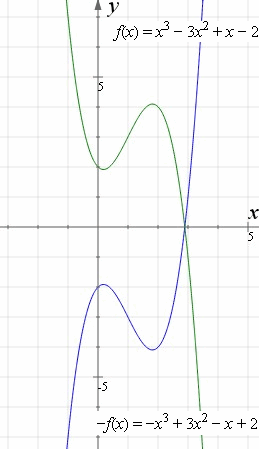
• Rotate about x axis, then y axis, then z axis But any sequence works!Fig 2 is its reflection about the xaxis Every point that was above the xaxis gets reflected to below the xaxis And every point below the xaxis gets reflected above the xaxis Only the roots, −1 and 3, are invariant Again, Fig 1 is y = f(x) Its reflection about the xaxis is y = −f(x) Every yvalue is the negative of the original f(x)This video explains to graph graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect th




Reflection Over X Axis Y Axis Equations Examples Graph Video Lesson Transcript Study Com




Reflection
Function Transformations Reflections Across the xaxis and yaxis This video explains how to graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect the graph of f(x) Show Stepbystep Solutions Reflecting FunctionsDemonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y = m x c Draw Dist Auto Flip Share this GraphM A B ¯ = 3 m A ′ B ′ ¯ = 3 m B C ¯ = 4 m B ′ C ′ ¯ = 4 m C A ¯ = 5 m C ′ A ′ ¯ = 5 Though a reflection does preserve distance and therefore can be classified as an isometry, a reflection changes the orientation of the shape and is therefore classified as an opposite isometry You can see the change in orientation by the order of the letters on the image vs the preimage




Algebra Precalculus Inverse Function Reflection In Y Axis Mathematics Stack Exchange




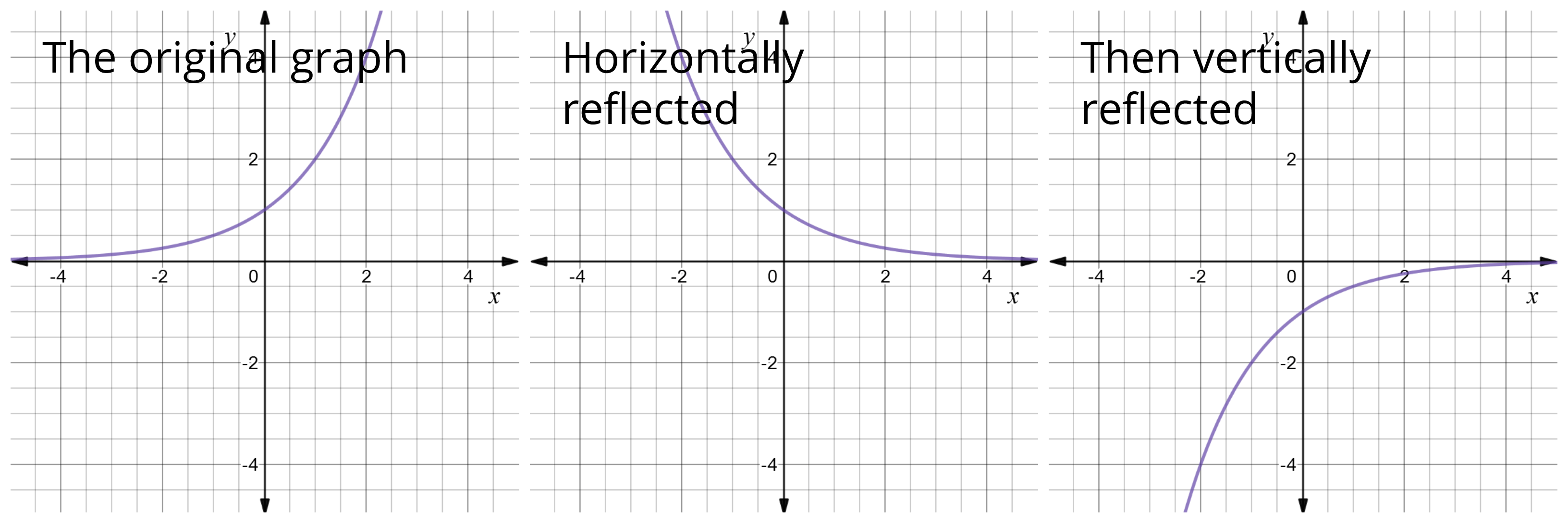
How To Reflect Quadratic Equations Video Lesson Transcript Study Com
1 Reflection Over The XAxis Sets of Coordinates If you have a set of coordinates, place a negative sign in front of the value of each yvalue, but leave the yvalue the same (4, 6), (2, 4), (0, 0), (2, 4), (4, 6) (4, 6), (2, 4), (0, 0), (2, 4), (4, 6)So as predicted, it's a reflection it's a reflection of our parent graph y equals 2 to the x This is y equals 2 to the negative x Just remember, any time you take a function and you replace its x with a x, you reflect the graph around the y axis And that's it more I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0 If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^x



Assignment 2 Transforming Parabolas



Graphs Of Exponential Functions
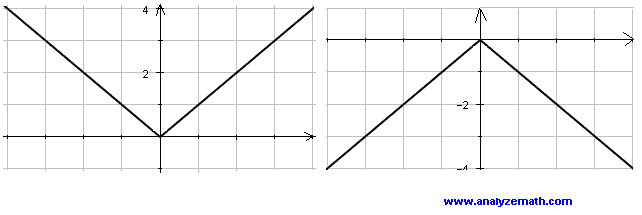
Well, because we're doing negative Fx That means all of our why values are going to be the opposite sign Well, if you were a negative value for Y at first, when you multiply by a negative will become positive And if you multiply a positive value by a negative that will become negative So no, this this graph flips over the X axis So in this case, what we now know is that negative F of The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4) Reflect Over XAxis or YAxis If there is a negative outside parentheses, then reflect over the xaxis, or vertically (all the yvalues become negative) ex f(x) = x2



Discovering Advanced Algebra Resources
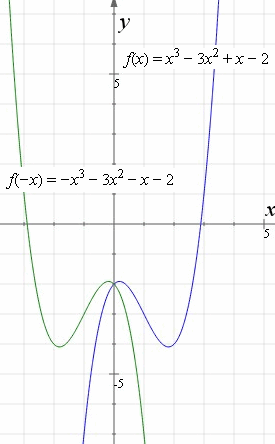



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
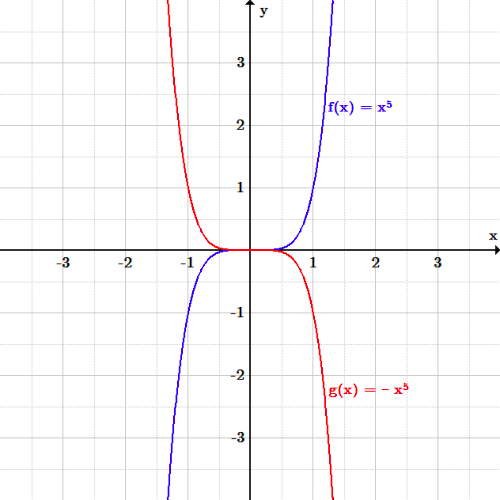
A reflection takes whatever graph we have and flips it across either the xaxis or yaxis The graph below has an example of each of these reflections with respect to our parent graph Notice that there are only two graphs In some cases, the reflection acroff one of the axis, just gives back the original equation(Rotation about z, x' and z') Note TaitBryan vs Proper Euler TaitBryan rotations rotate about three distinct axes (x y z) Proper Euler angles share axis for first and last rotation (z x z)A math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axis



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com




Objectives Be Able To Graph A Quadratic Function In Vertex Form Be Able To Write A Quadratic Function In Vertex Form 2 Ways Ppt Download
This is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableIt is reflected across the y axis, so the negative goes inside of the function f(x) = 3 x 6Given a function f ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axis
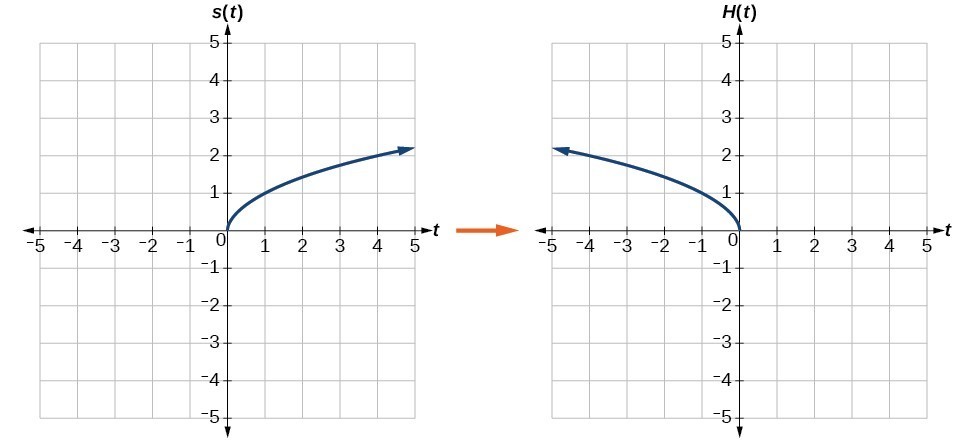



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
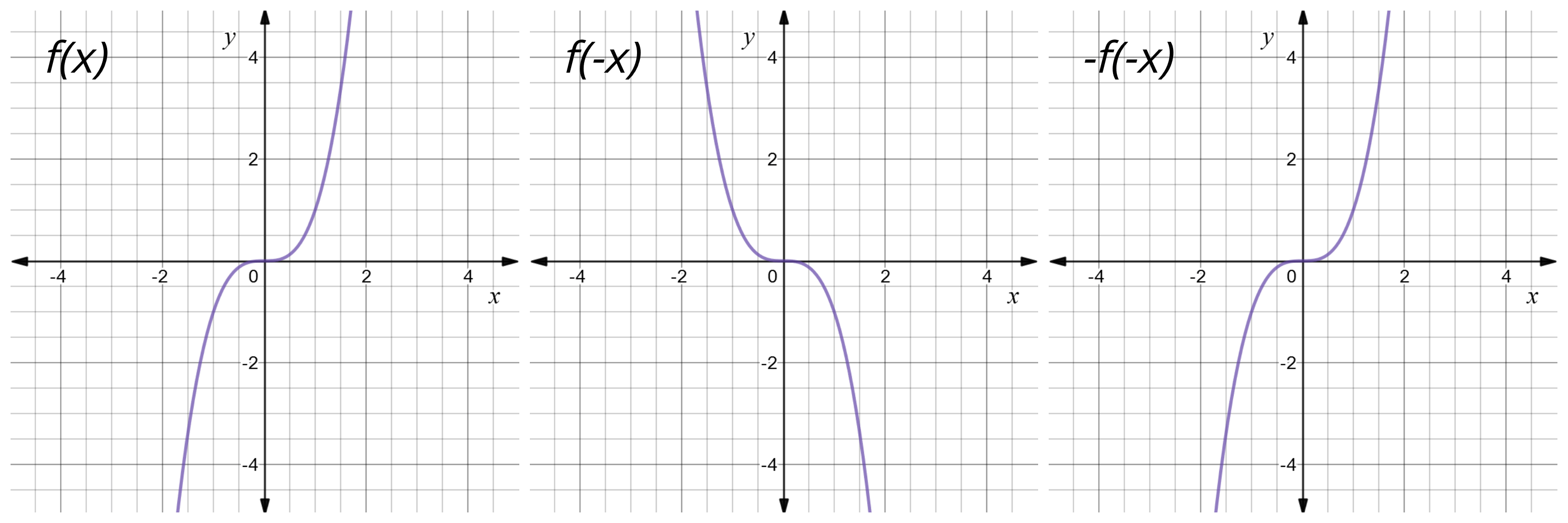



Reflect Function About X Axis F X Expii
The transformations done are option A A reflection over the yaxis, then a reflection over the xaxis Stepbystep explanation Step 1 First, we plot the points of triangle ABC and A''B''C'' The points of triangle ABC are A (8, 5), B(4, 3), and C(4,7) The points of triangle A''B''C'' are A'' (8, 5), B'' (4, 3), and C'' (4,7) The points of both triangles ABC andA reflection across xaxis is nothing but folding or flipping an object over the x axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directions




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
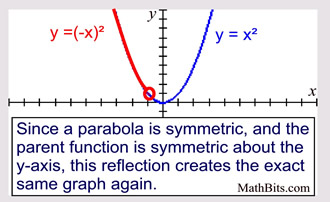



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
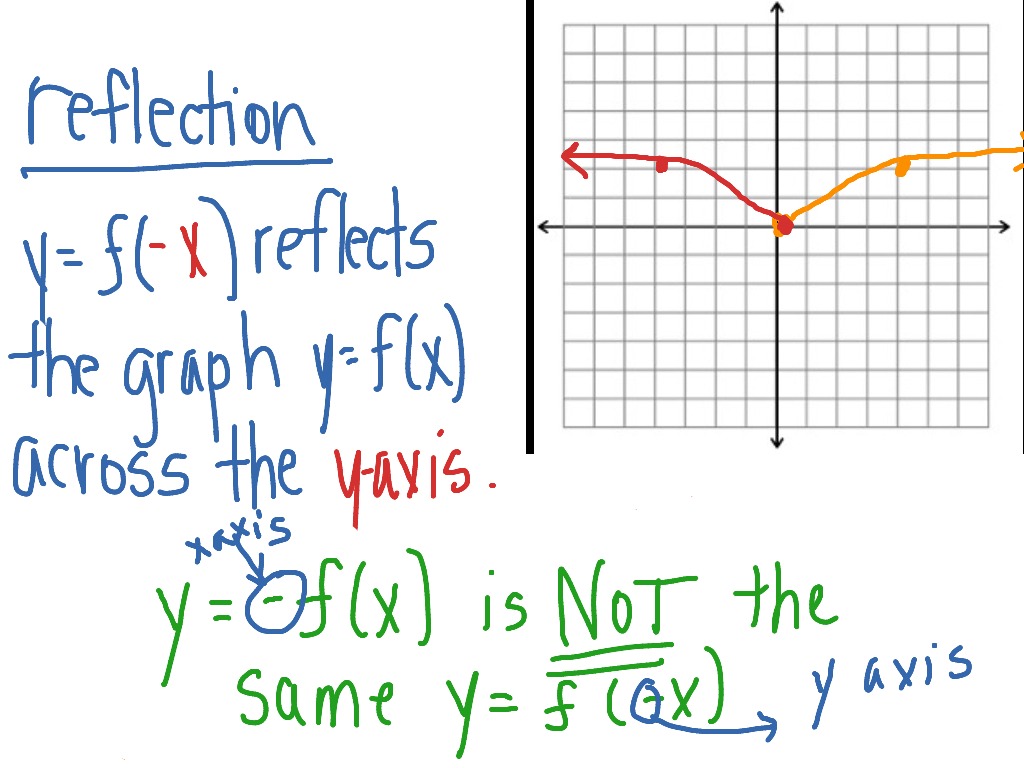



Reflection Across The Y Axis Math Functions Showme
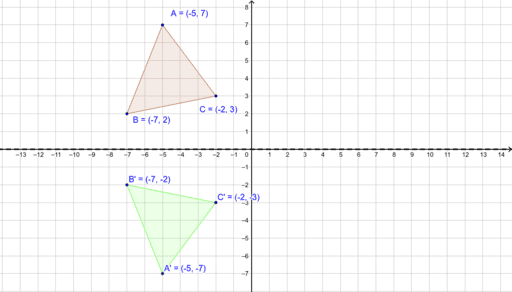



Reflection Over X Axis Geogebra
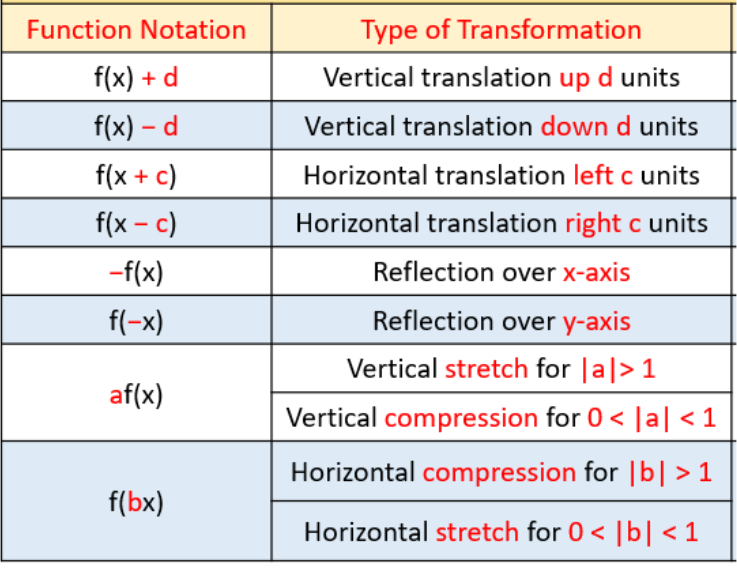



Transformations Of Equations Katelyn Miller Library Formative
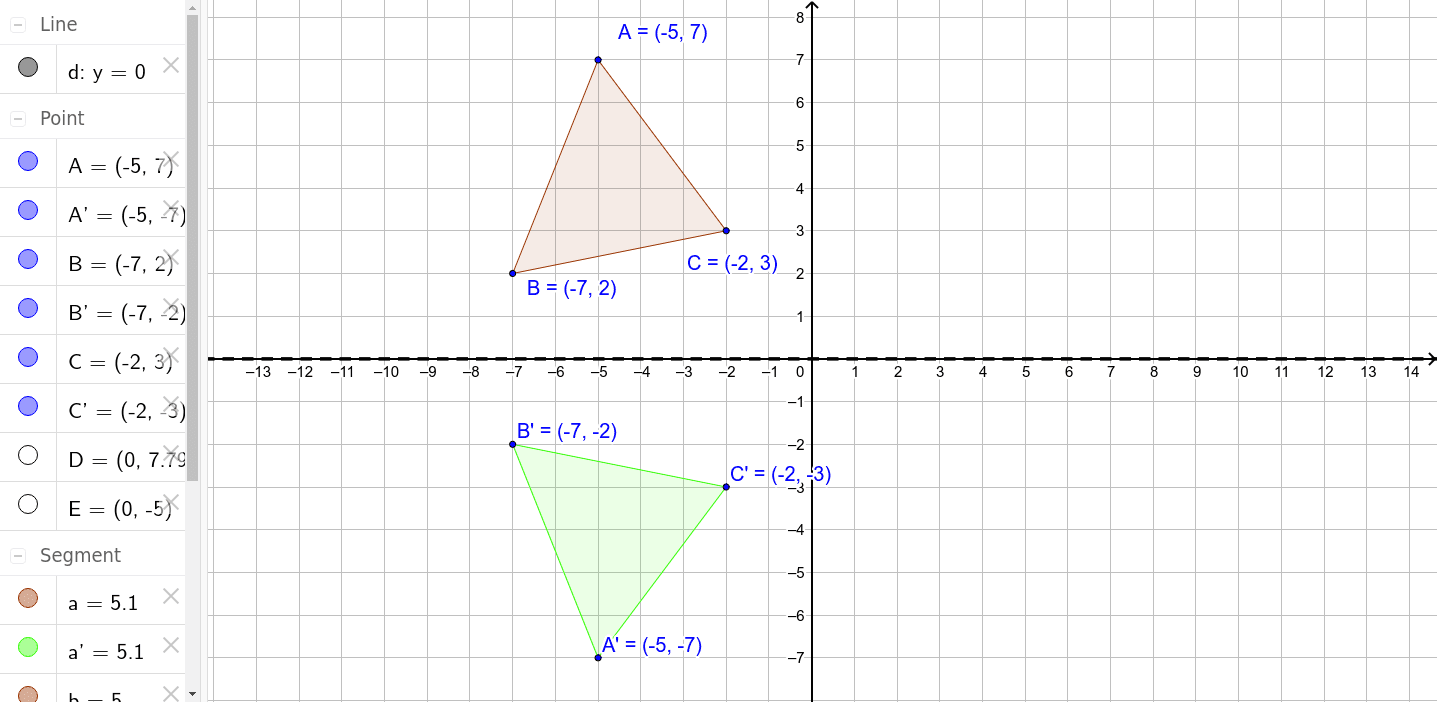



Reflection Over X Axis Geogebra




Reflections




Today In Pre Calculus No Calculators Needed Notes Rational Functions And Equations Transformations Of The Reciprocal Function Go Over Quiz Homework Ppt Download



Parabola Scalings And Translations Zona Land Education
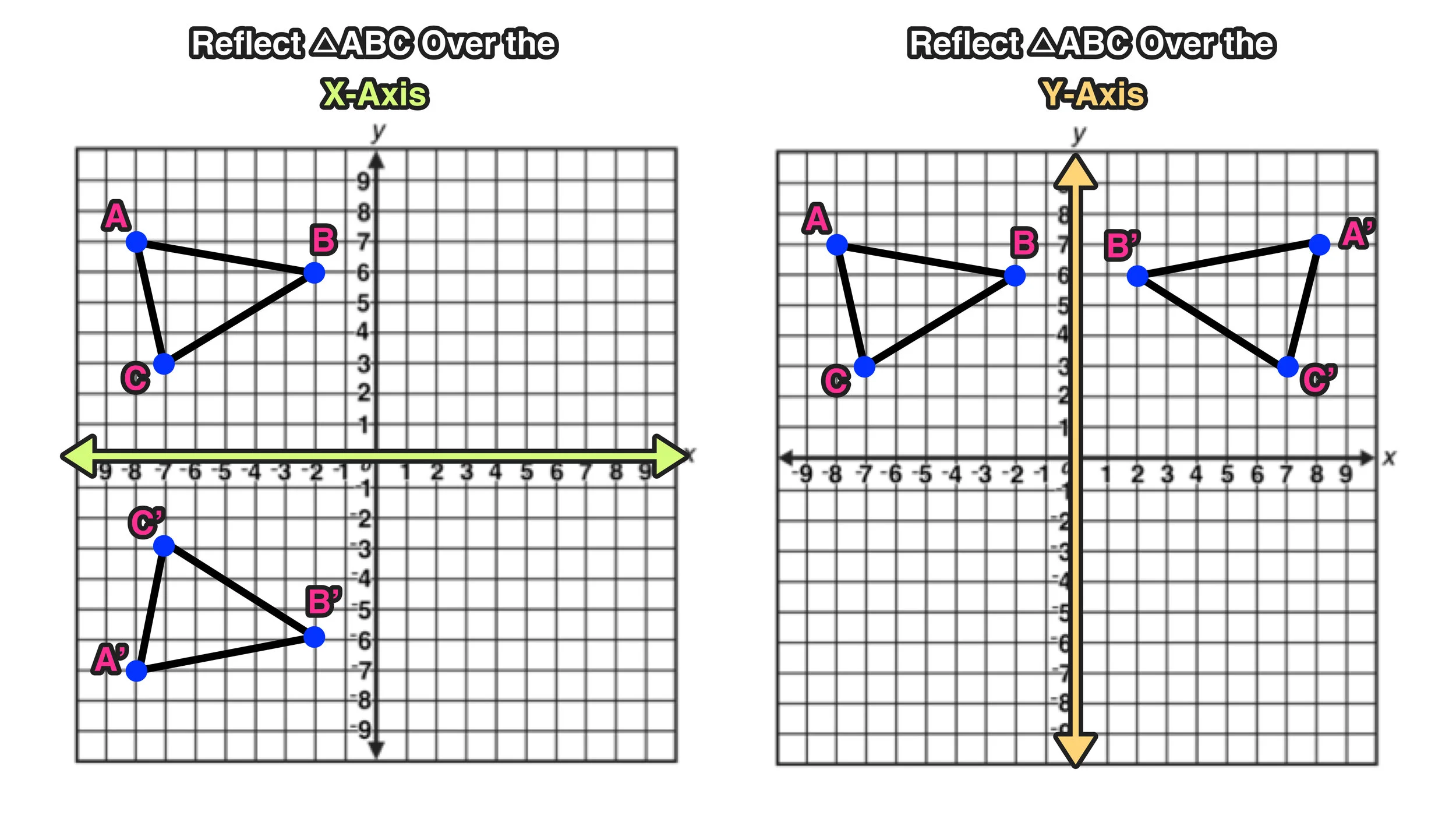



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Using Transformations To Graph Functions
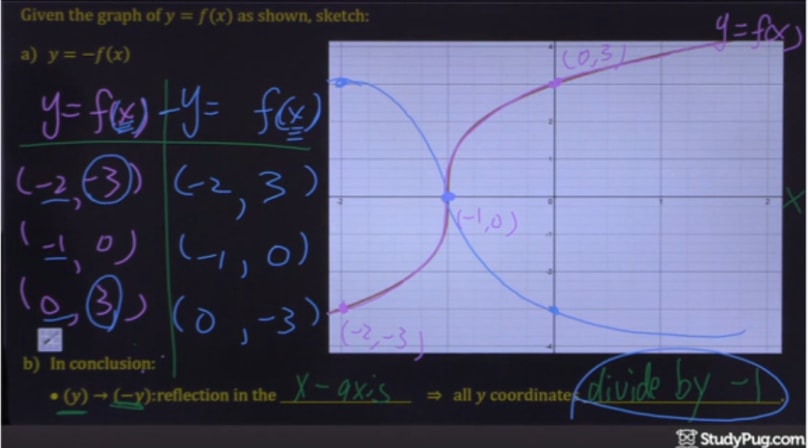



How To Reflect A Graph Through The X Axis Studypug



Operations On Functions Reflections And Rotations Sparknotes
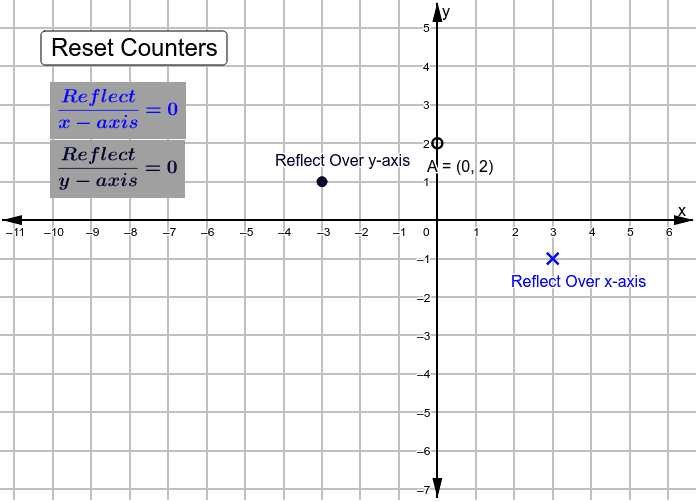



Reflect Points Across X Axis Y Axis Geogebra



Ch 3 4



Horizontal Stretch
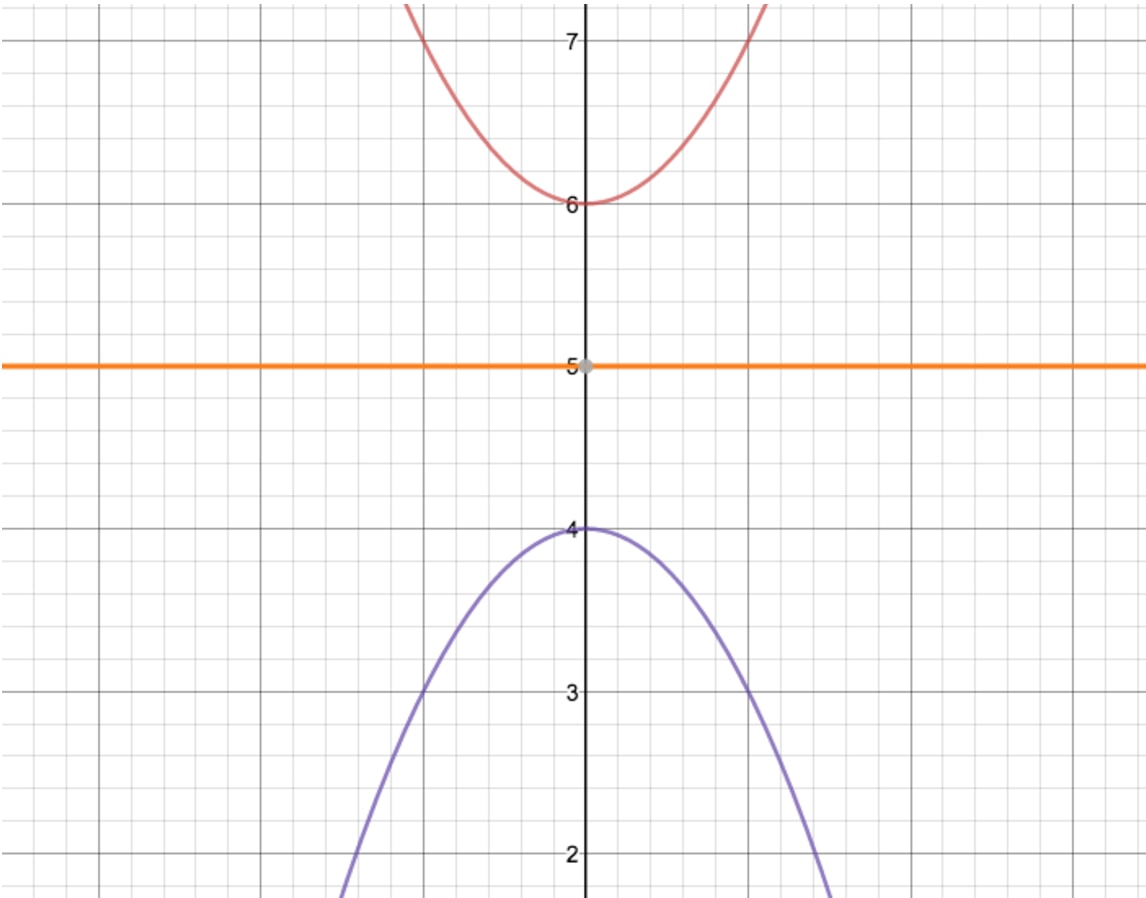



How To Reflect A Graph Through The X Axis Studypug




Graphing Reflecting Functions Video Lesson Transcript Study Com




The Transformation Of The Graph Of A Quadratic Equation Matherudition



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
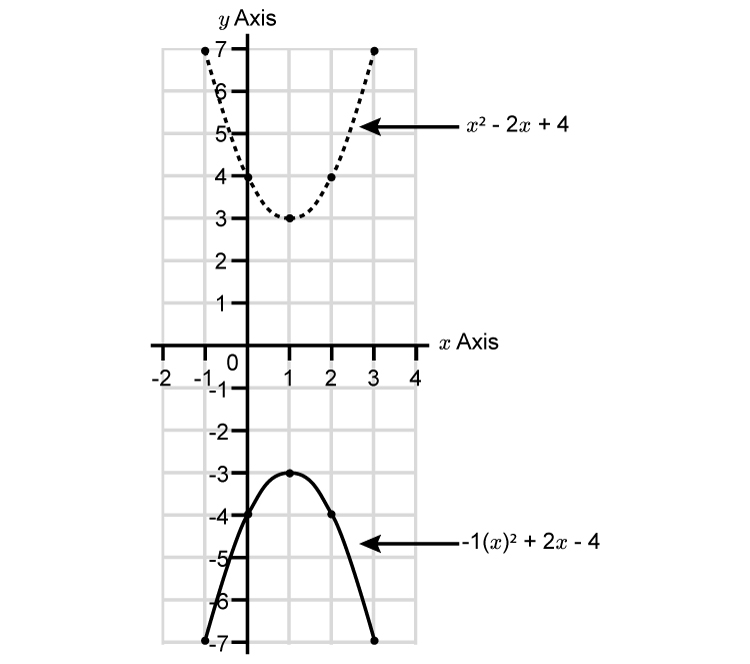



Reflecting More Difficult Parabolas Mammoth Memory Maths




Reflection Mathbitsnotebook A1 Ccss Math



A Review Of Logarithms




Translation And Reflection Learning Math Will Lead To Success



Reflect Function About Y Axis F X Expii



Reflections Over The X Axis And Y Axis Explained Youtube




Reflection Rules How To W 25 Step By Step Examples



Transformations Reflecting Over The X Axis




Scaling Reflecting Parabolas Video Khan Academy



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
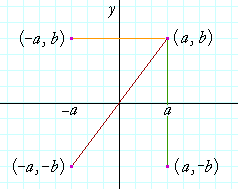



Reflections Of A Graph Topics In Precalculus



How To Reflect A Graph Through The X Axis Studypug



Graphing By Translation Scaling And Reflection



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Across The X And Y Axis Youtube



Transformations Ib Math Stuff
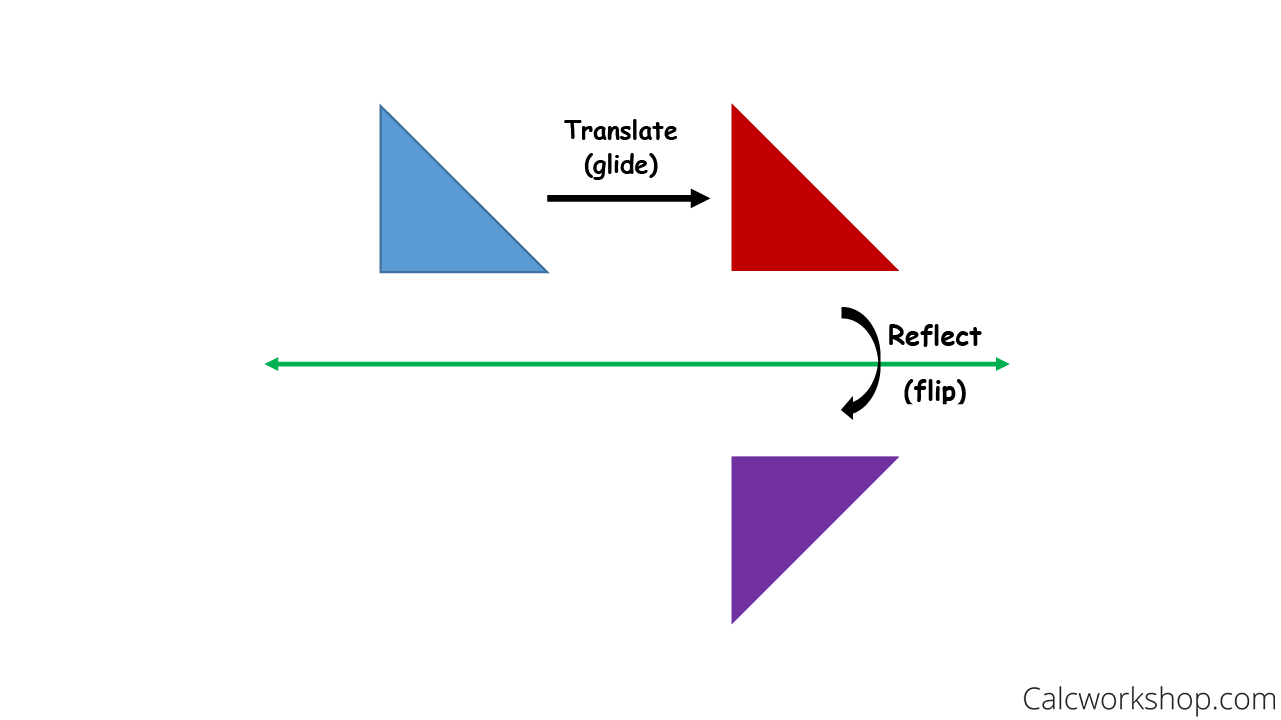



Reflection Rules How To W 25 Step By Step Examples



Does Reflecting The Parabola Across The X Axis Change The Axis Of Symmetry Quora
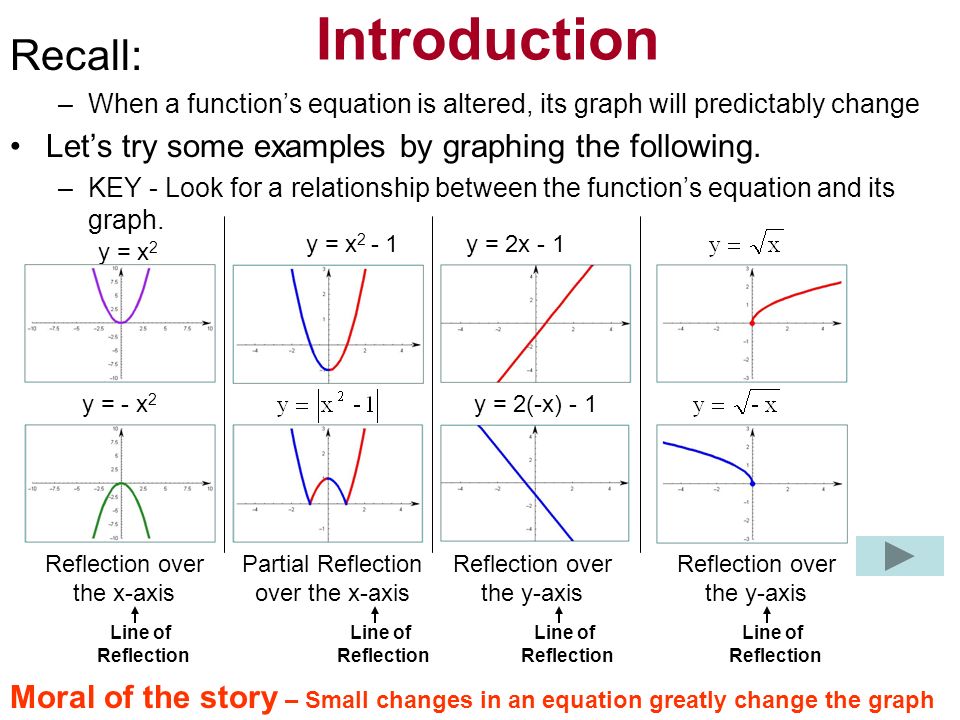



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
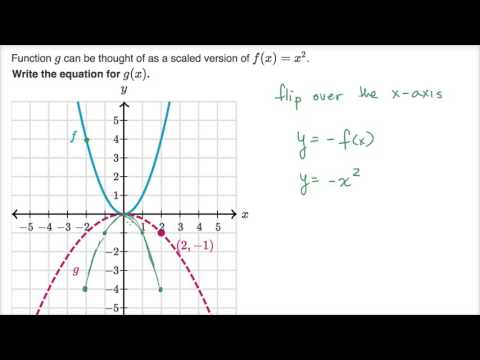



Scaling Reflecting Parabolas Video Khan Academy



How To Reflect Quadratic Equations Video Lesson Transcript Study Com
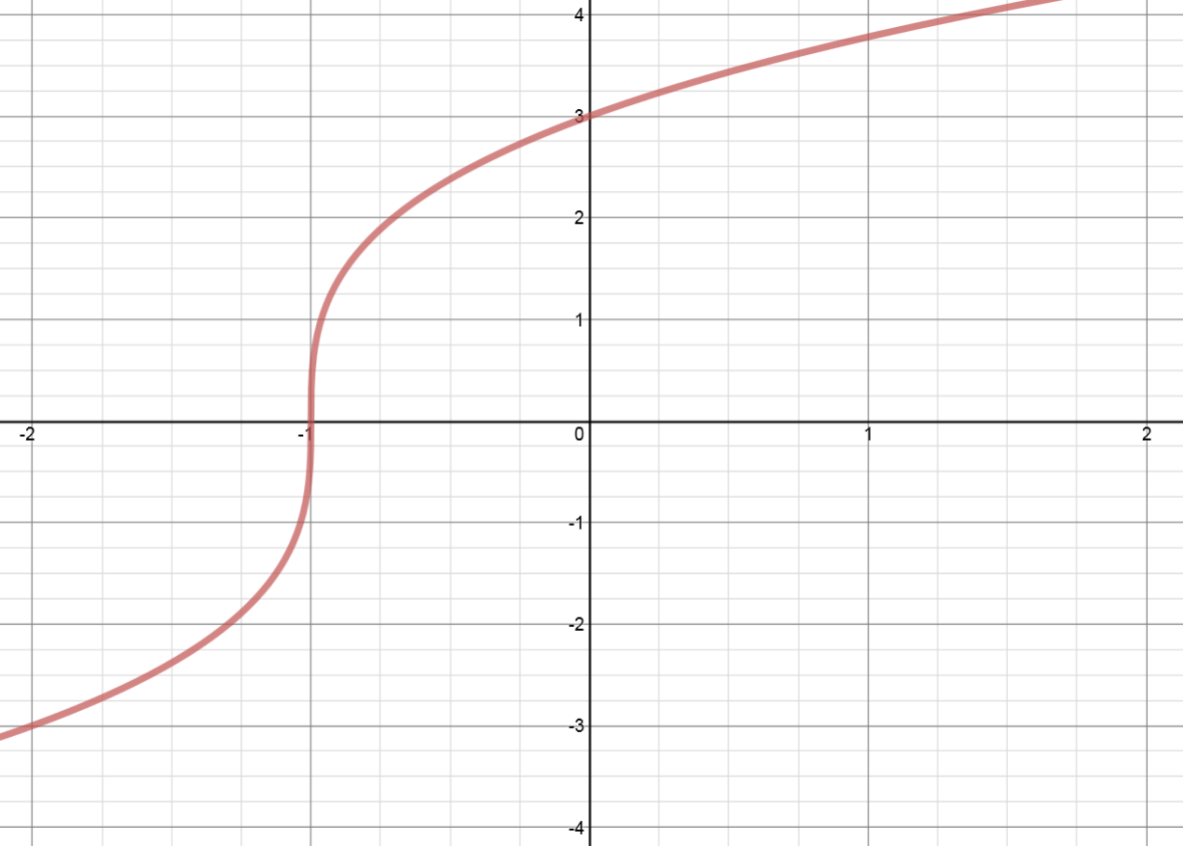



How To Reflect A Graph Through The Y Axis Studypug
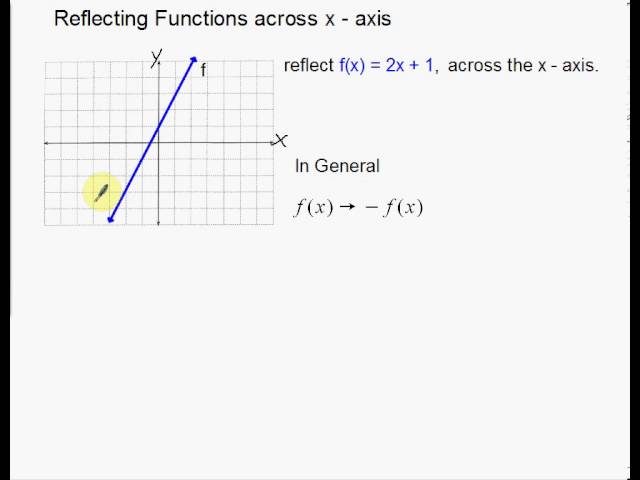



Linear Reflections Across X And Y Axis Youtube



Assignment 2 Transforming Parabolas
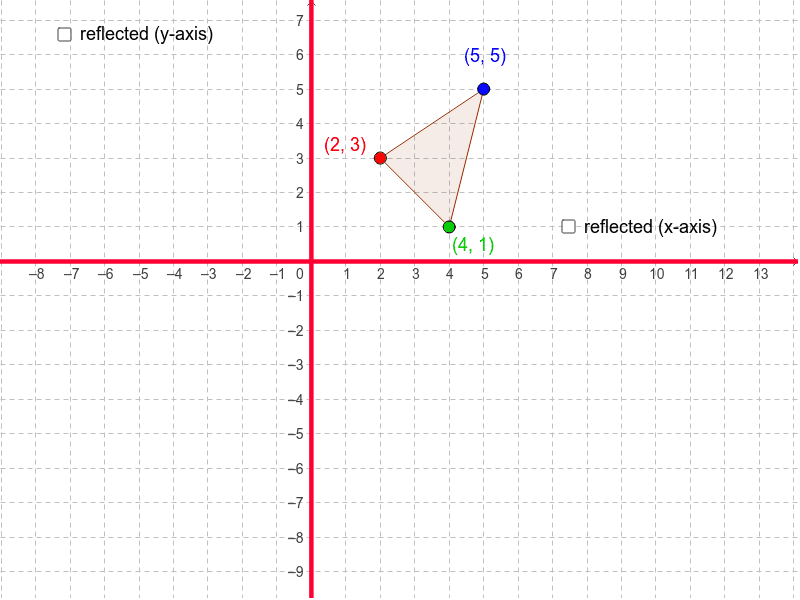



Reflection In The X Axis And Y Axis Geogebra




Warm Up Write The Equation In Vertex Form Of The Quadratic Equation That Has Been 1 Shifted Right 7 And Down Reflected Across The X Axis And Shifted Ppt Video Online Download
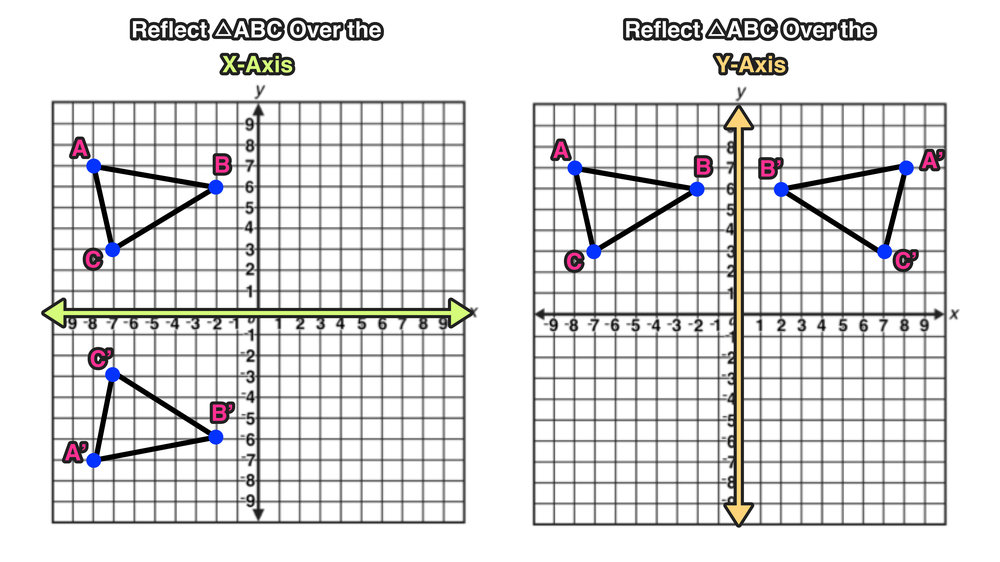



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




The Transformation Of The Graph Of A Quadratic Equation Matherudition



1



Reflections Pd1 Math 15 16




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
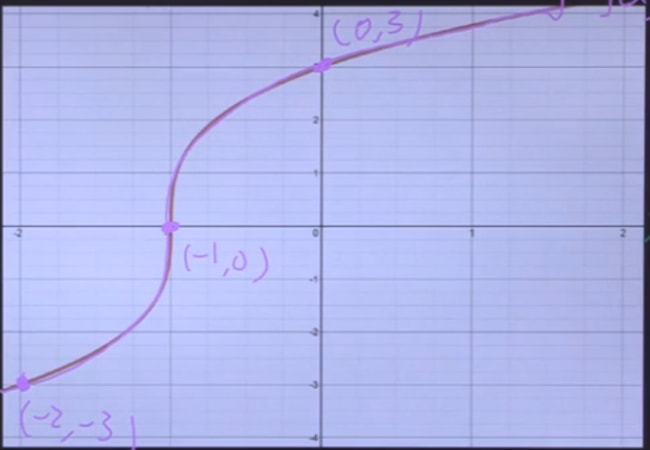



How To Reflect A Graph Through The X Axis Studypug
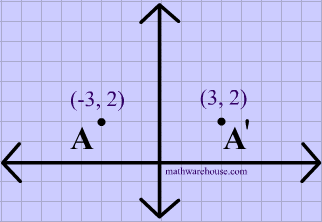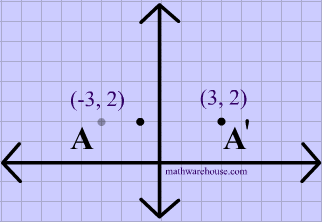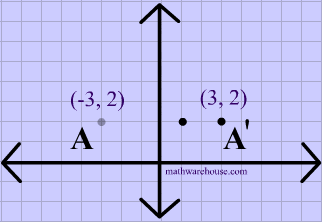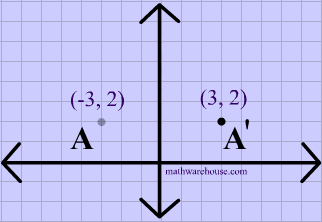



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



2



Operations On Functions Reflections And Rotations Sparknotes



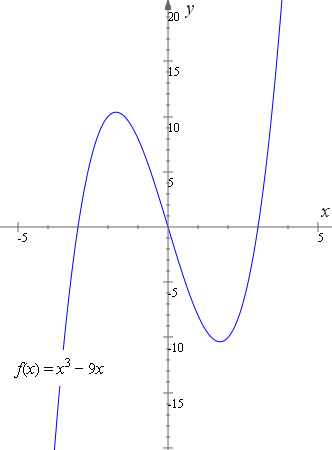
Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




Learn About Reflection Over The Line Y X Caddell Prep Online
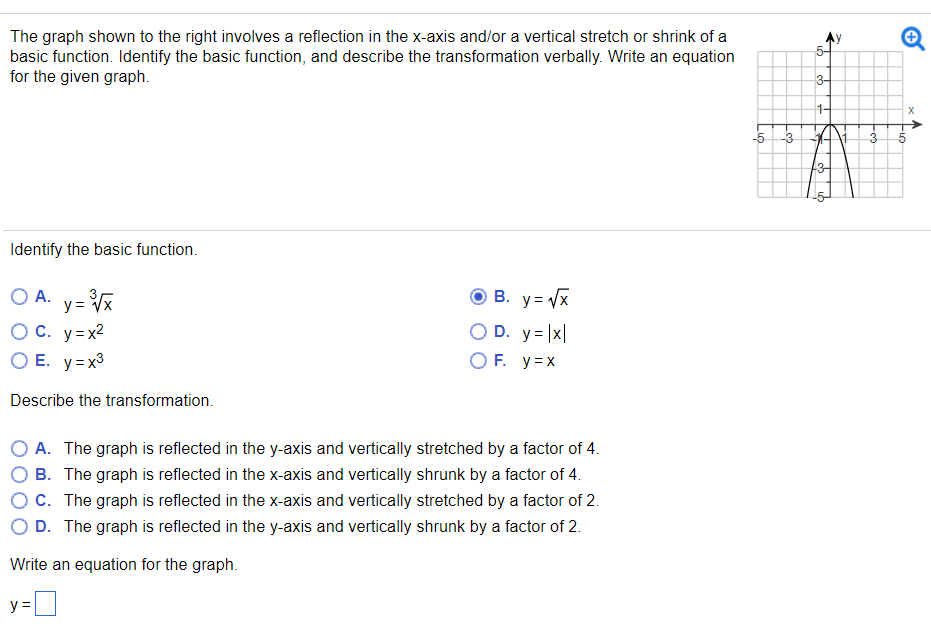



Solved The Graph Shown To The Right Involves A Reflection In Chegg Com
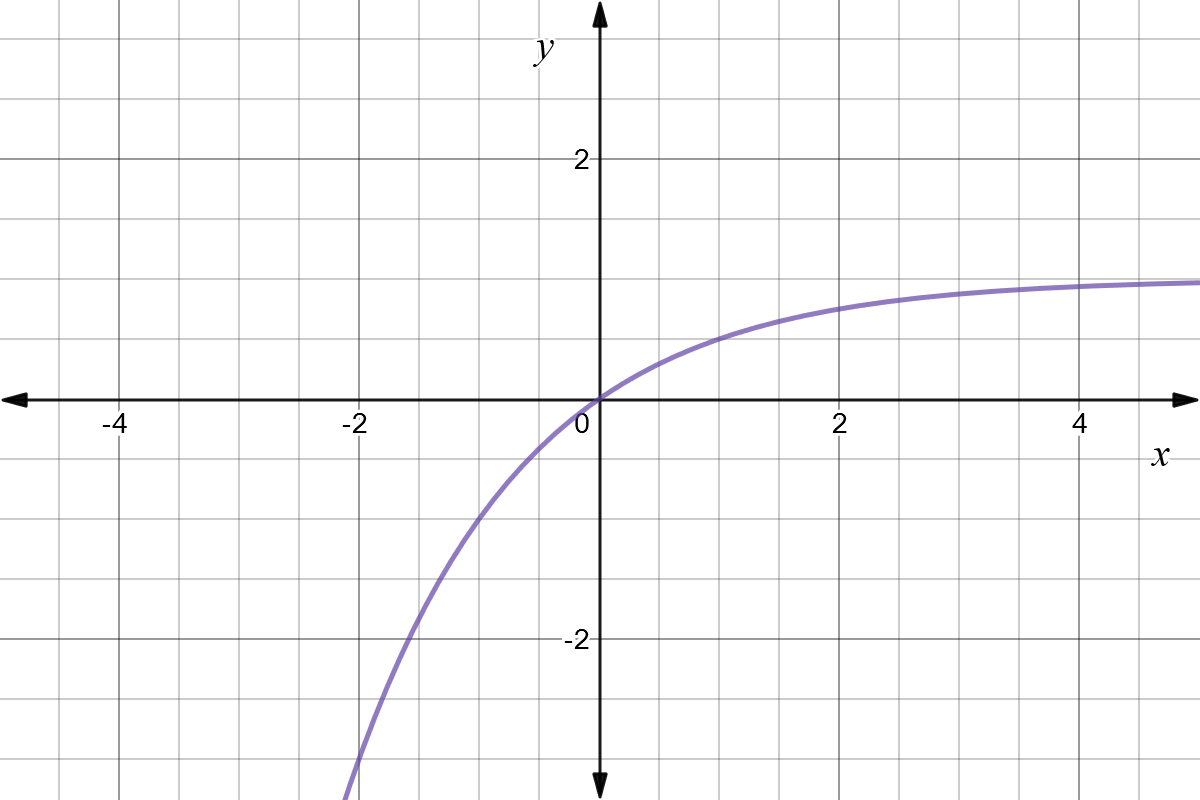



Reflect Function About Y Axis F X Expii
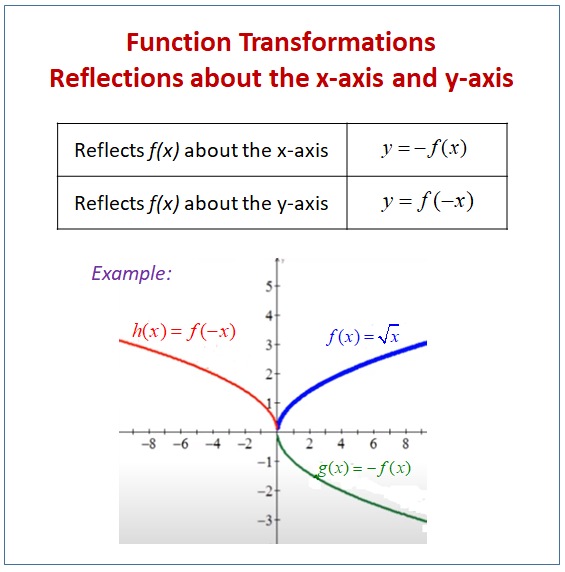



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities
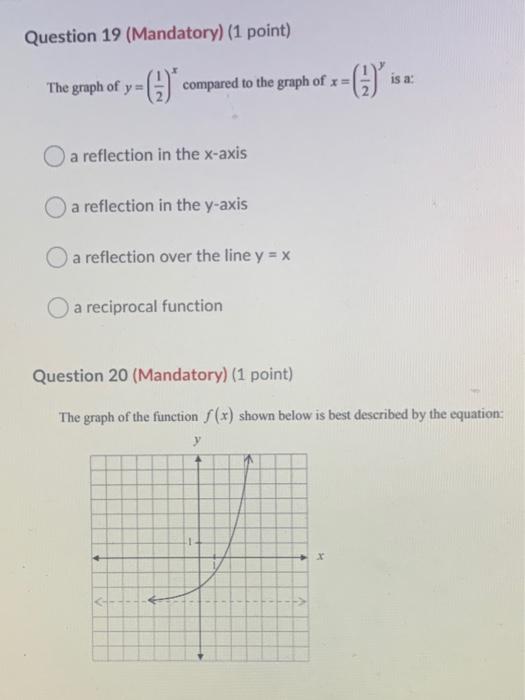



Solved Question 19 Mandatory 1 Point Is A The Graph Of Chegg Com




Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download




Transformations Boundless Algebra
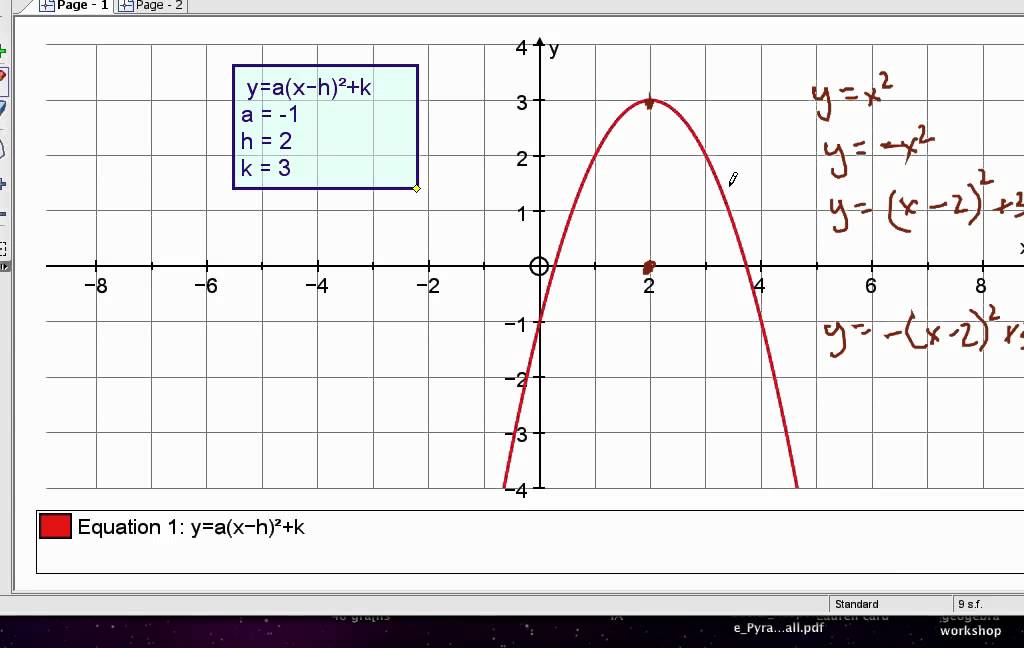



2 02 0 Reflection Over X Axis Mov Youtube




Reflection Mathbitsnotebook A1 Ccss Math




Reflect Function About Y Axis F X Expii



1




Cartesian Coordinate System Wikipedia



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflecting Functions Examples Video Khan Academy
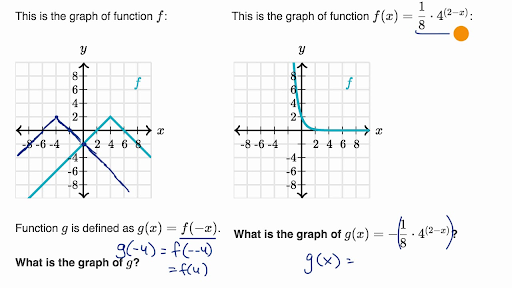



Reflecting Functions Examples Video Khan Academy




Reflecting Figures In Coordinate Space Krista King Math Online Math Help




Scaling Reflecting Absolute Value Functions Equation Video Khan Academy




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Harper Gallery Y Axis Chart



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




The Transformation Of The Graph Of A Quadratic Equation Matherudition


