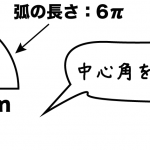
だから、扇の面積を求めるためには中心角を求める必要があるよ。中心角の求め方を忘れてしまった人は、扇形の中心角の求め方3パターンピザでわかるを見てね 中心角は、円と扇の円周比を使って $2\pi r 2\pi l = x 360$ ∴ $2\pi l x = 7 \pi r$ 底面の半径が3cmなので、円周=直径× π =6 πcm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 π cmです。 そこから、半径12cm&孤の長さ6 π cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。数学・算数 扇形の中心角と円弧の求め方 扇形の中心角と円弧の求め方を教えて下さい(~_~;) 双方わからない状態です。(半径はわかります) 質問No

2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
扇形 中心角 求め方 面積
扇形 中心角 求め方 面積-より厳密には、円の劣弧(中心角が180 弓形の面積 a は扇形の面積から、三角形部分の面積を引いて = = (()) で求められる。あるいは中心角を度数法で測るならば = である。 円板全体の面積 s = πr 2 との比をとれば、 = = となる。 応用 面積公式は、部分的に充填された円筒形の貯蔵タンクの弧の長さと面積の公式 <証明> 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。




扇形の中心角の求め方を教えてください Clear
円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l それぞれについて詳しく見ていき① おうぎ形の弧の長さ = 直径 × π × 中心角 360° より 弧の長さ = 18×π× 64 360 = 16 5 π 答 16 5 π cm ② おうぎ形の面積 = 半径 × 半径 × π × 中心角 360° より 面積 =9×9×π× 64 360 = 72 5 π 答 72 5 π cm 2 確認問題 次の問いに答えよ。 半径6cm, 中心角30°のおうぎ形の弧の長さを求めよ。中心角の単位は「度」でしょうか? そうであれば、ラジアンに直して、公式に代入ください。参考)角度の換算 度≒ ラジアンなので、 例えば面積 S=1/2*()^2*(sin())= と求められます。
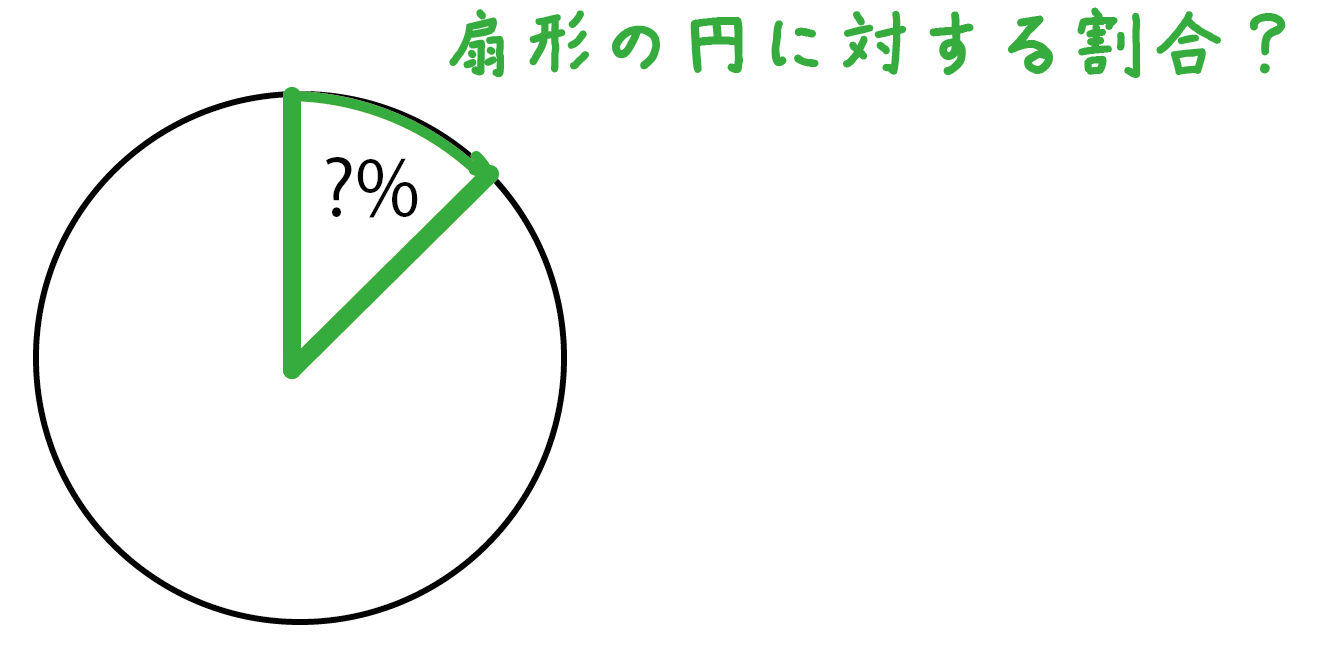
円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。 扇形の弧の長さが分かっているときは、 円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。 扇形の割合が分かったら、中心角を求めていきます。 扇形の中心角(PDF) Tweet 登録カテゴリ 扇形 の 中心 角 求め 方 おうぎ形の中心角を求める問題でわかっている数字が変わると求め方がわからなくなります このqaでは 進研ゼミ中学講座 会員から寄せられた質問とその回答の一部を公開しています 側面である扇形の面積を求めようとすると扇形の公式から分かるように 中心角が必 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。半径rの円の面積の θ / 360 倍の大きさで求める方法です。頭の中に大きな円はイメージできていますか?
演習問題で理解を深める! (1)半径6㎝、中心角1°のおうぎ形の弧の長さと面積を求めなさい。 (1)解説&答えはこちら 答え 弧の長さ: 面積: 弧の長さを求めるためには の公式にあてはめます。 円の面積を求めるためには の公式にあてはめます 6 半径3cm、弧の長さ5πcmの扇形の面積の求め方を詳しく教えてください 7 半径と面積が分かっているときの中心角の求め方 8 半径12cmで中心角が、60度のおうぎ形について、面積を求めなさい!★扇形の中心角の求め方★途中式をていねいに解説!面積、弧の長さから求める方法|中学数学・理科の学習まとめサイト! 扇形 ~弧の長さ、半径から中心角を求める~ 高精度計算サイト 最も人気のある 円錐




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
扇形の面積はわかるのですが三角形の面積の求め方がわかりません。 答えは25π+40cmです。解説お願いします 数学・0閲覧 共感した ログインして回答 回答受付中の質問 高校数学 来年の高校数学の教科書について 各出版社のホームページで、来年令和4年度の教科書について 数学1、数学A 扇形の中心角を求める公式 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね はかせちゃん はかせOfficial円錐の表面積の求め方 (2) 円錐の表面積を求めますが、展開図ですね。 円錐の展開図は扇形と円となります。 表面積は、扇形の面積と、底面の円の面積を足すだけです。 扇形の面積は普通に求めれば、中心角が\(\,150°\,\)と分かっているので




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
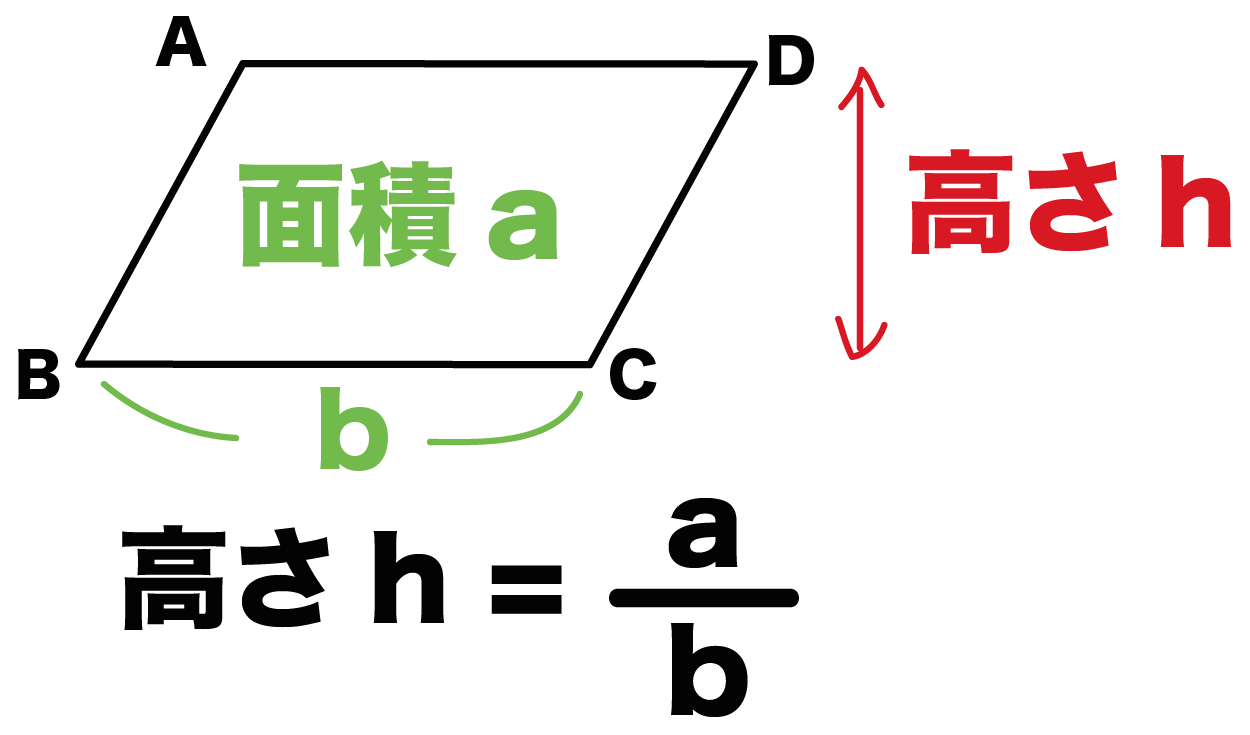
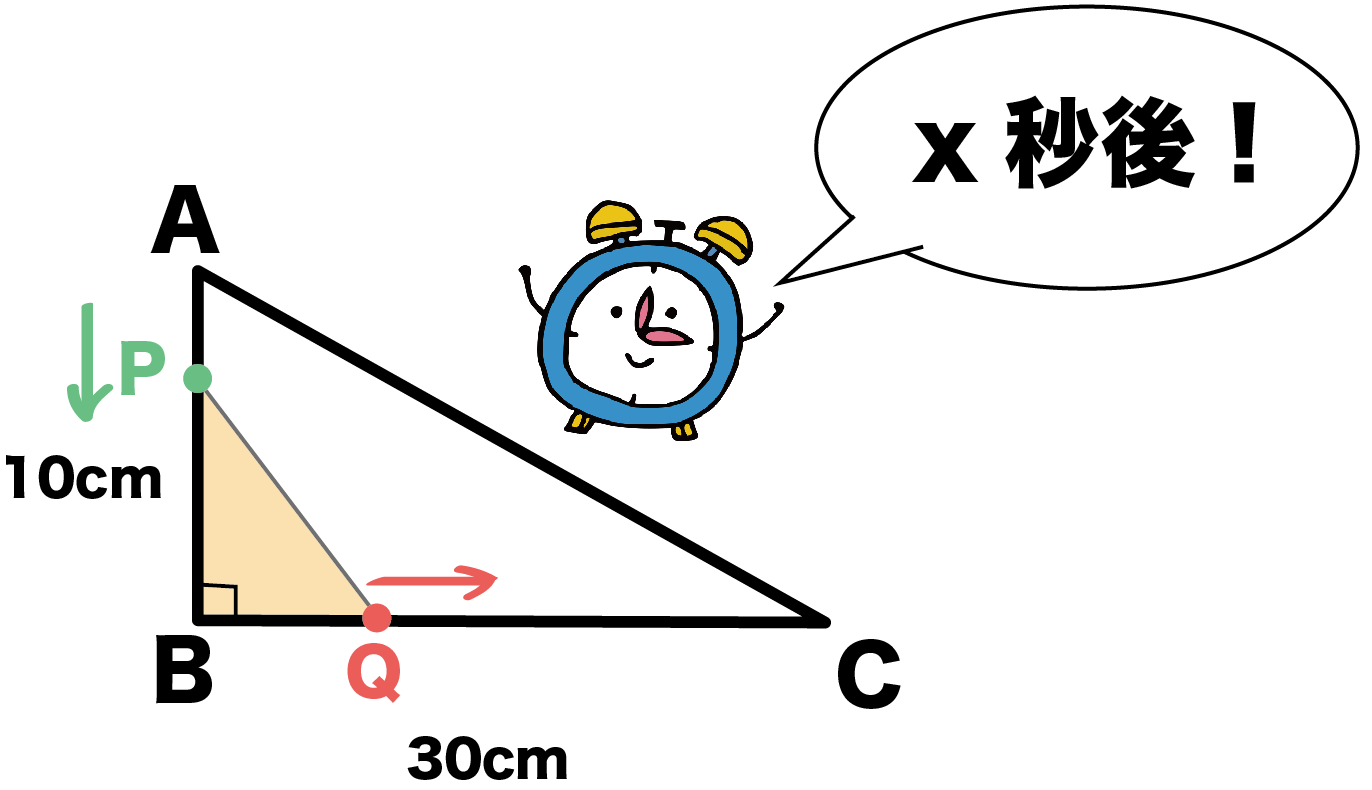
なぜ公式がつかえるのか?? 一生使える!扇形の面積の求め方の公式! 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360 になるんだ。 つまり、はじめに 半径が「r」、中心角が「θ」である扇の面積「S」は で求めることができました。 ここでは、 中心角「θ」が与えられていない その代わりに弧の長さ「l」は与えられている 場合に扇の面積を求める公式を紹介しましょう。 半径「r」、弧の長さが「l」の扇の面積「S」は次のように求めることができます。 この公式を実際に求めてみましょう。 中心角が分からない扇形の面積の求め方の裏ワザ テーマ: ブログ 今回は、勉強のことだよ。 中心角が分からない扇形の面積の求め方の裏ワザだよ。 ↓これ この扇形の弧の長さを15㎝、 AからCの長さは10cmにするよ。 この問題を普通にやると、



カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



扇形の面積
ベストアンサー:8π=2π×6×x/360 8π=12πx/360 両辺に360をかける 12πx=π 両辺を12πで割る x=240 6 3/28 1040扇形の弧の長さと面積の求め方としては、どのように計算すればいいのでしょうか。 扇形の弧の長さや面積を計算する場合、必 楕円の弧長の求め方 お客様の声 アンケート投稿 よくある質問 リンク方法 楕円扇形の面積 00 / 0件 表示件数 メッセージは1件も登録されていません 扇形の面積は、同じ半径の円の面積に中心角の割合をかければ求められます。 扇形の面積の求め方 \begin{align}\text{(扇形の面積)} = \text{(円の面積)} \times \text{(中心角の割




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋
どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角/180 となります。 2 1005 男 / 40歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 上と同じ問題で考えてみると おうぎ形の面積は3πで中心角は x です。 それに対して、同じ半径 (3㎝)を持つ円の面積と中心角を考えると9πと360°になります。 ※円の中心角は常に360°です。↑この問題の解き方(途中式)を 9 この半円の半径と、 EHGの面積の




円 扇形 の面積 周や弧の長さの公式 数学fun
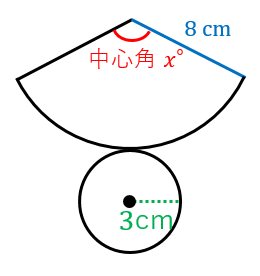



円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
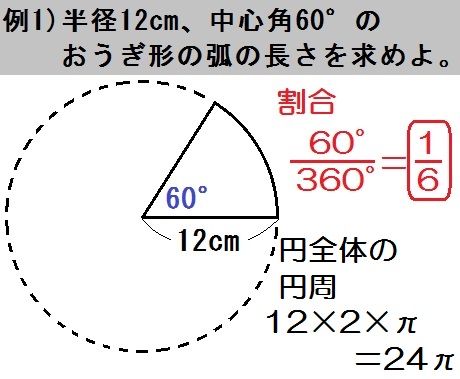
「扇形の中心角の求め方」の公式 ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、 x = 180L/πr になるってやちゃんとやり方を覚えれば難しくないからね しっかりと学んでいってくださいな ちなみに おうぎ形の中心角を求める方法は大きく分けて3パターンあります。 そのため、弧の長さを求めるには、円周の長さを求める公式に「円全体に対する扇形の割合」をかければよいことになります。扇形の面積 S × a ∘ 360 ∘ 例1) 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから、直径で計算する円周の式に




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe



半径10センチ 中心角90 の扇形oabの内部にoa Obを直径と Yahoo 知恵袋
です。 (πは円周率:π=←無限に長い小数になるからギリシャ文字πで表すことになっている) 半円の面積は,円の面積の半分だから 3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角の扇形の面積は,円の面積のx/360だから 例題1 半径がa(cm2)で中心角が45°の扇形の面積S(cm2)は 例題2 中心角を \(x\) とすると、扇形の面積公式を利用し $$\pi \times 6^2\times \frac{x}{360}=12\pi$$ という方程式を作ることができます。数学Ⅱ(三角関数):円弧の長さと扇形の面積(弧度法) オンライン無料塾「ターンナップ」 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ(ラジアン)の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の
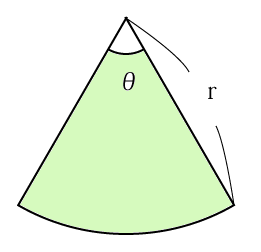



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
半径16cmで中心角315°のおうぎ形の弧の長さを求めよ。 半径12cmで中心角80°のおうぎ形の面積を求めよ。 半径10cmで中心角°のおうぎ形の面積を求めよ。 半径 9 2 cmで中心角160°のおうぎ形の面積を求めよ。 半径3㎝、中心角1°のおうぎ形がある。 弧の長さをですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2扇形の面積は、「 半径が等しい扇形の面積は、中心角に比例する 」という性質を使って、円の面積 πr2 π r 2 に 中心角 360∘ 中心角 360 ∘ の 割合 をかけることで求められます。




おうぎ形 弧の長さ 面積 中心角の求め方 学習内容解説ブログ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
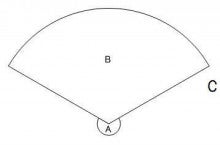



中心角が分からない扇形の面積の求め方の裏ワザ 爽のつぼやき




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題



半径8cm 中心角135 のおうぎ形の弧の長さと面積を求めてくださ Yahoo 知恵袋




半径9cm 面積18pcm の扇形の孤の長さと中心角の求め方を教えて欲しいです Clear



弧 の 長 さ の 求め 方 中学数学 円錐の 母線の長さ がわかる2つの求め方 Docstest Mcna Net




扇形の面積の求め方 公式と計算例




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月



3




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube



扇形の面積




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
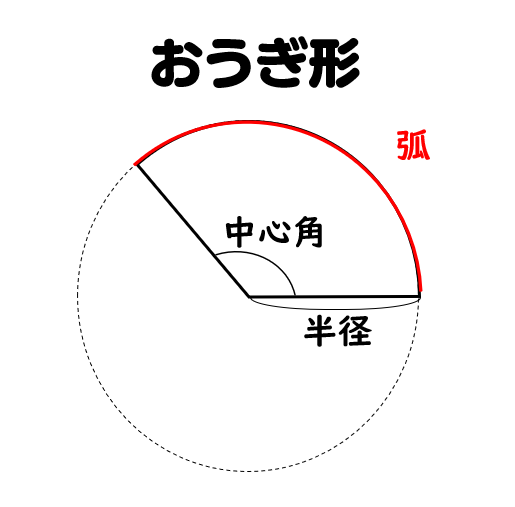



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



3




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear



カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear




扇形の中心角の求め方を教えてください Clear




半径9cm 面積18pcm の扇形の孤の長さと中心角の求め方を教えて欲しいです Clear




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



扇形の半径と面積が分かっているときの中心角の求め方を教えてください 例 Yahoo 知恵袋




扇型の求め方や中心角の求め方も分からないので 解説もお願いします この問題の答えは Clear



1




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



3




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ



半円と等しい面積の扇形の中心角は 算数解法の極意
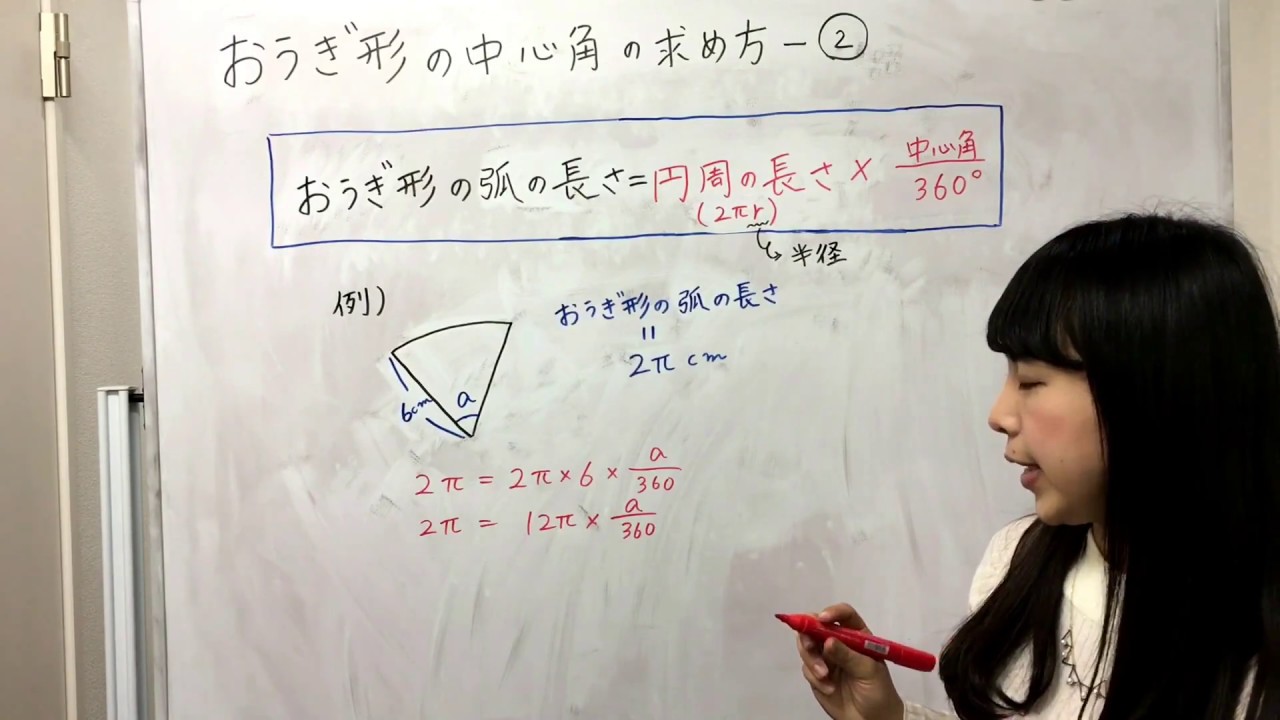



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
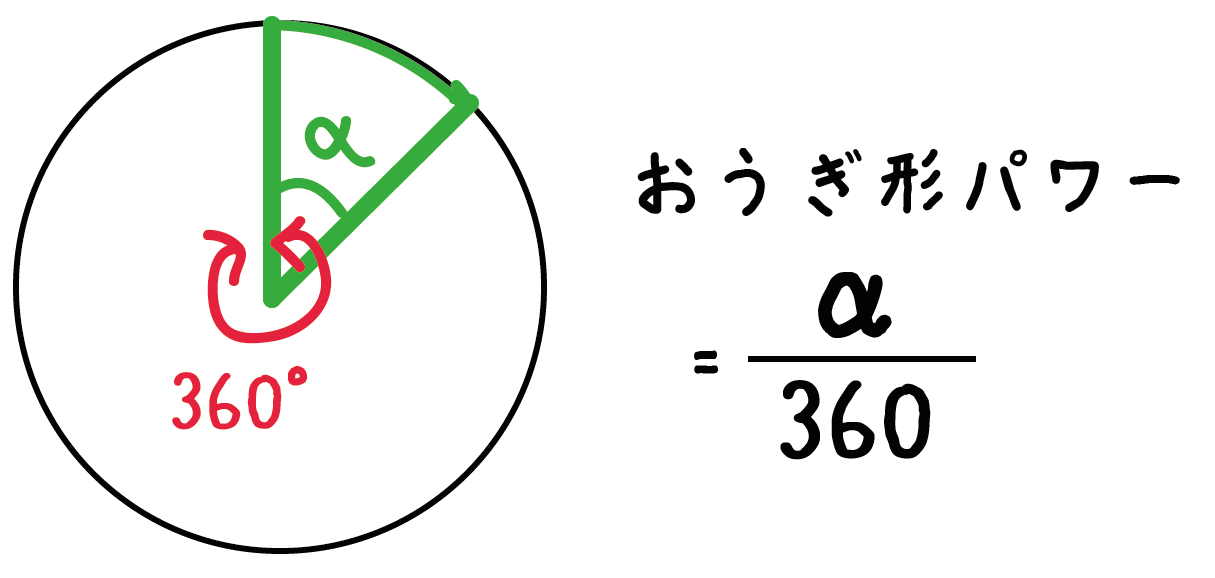



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形の面積の求め方 公式と計算例




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




なぜ扇形の面積にするという考えになるのですか 解説を見ても分かりませんでした Clear




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




扇形の中心角の求め方 面積と半径がわかっているパターン Youtube



扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題



扇形の面積




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



扇形の面積



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




これの表面積の求め方の解説をお願いしたいです W Clear




角錐 円錐の体積と表面積の公式 数学fun


